Coffea Analysis

Overview

Teaching: 20 min
Exercises: 60 min

Questions

What is the general plan for the analysis?

What are the selection requirements?

How do I implement additional selection requirements?

What are Coffea Processors?

How do I run an analysis with Coffea?

Objectives

Understand the general strategy for the analysis

Learn how implement basic selection requirements

Learn how to build Coffea Processors and run an analysis

Getting things prepared for this episode

I’m going to assume that you have stopped the Docker container from the last episode. If you have not, let’s walk through how to start things up and add one more piece of data.

Type out the following commands for this episode!

For this next section, you’ll be asked to type out the provided commands in a Jupyter notebook, a popular development environment that allows you to use python in an interactive way.

Please enter in these commands yourself for this episode.

To create or run the notebooks used in this episode, we will

Start the python docker container
- We assume that we have installed the necessary modules from the previous episode (e.g. coffea)
Clone a repository of some helpful utilities for this episode.
Launch Jupyter Lab.
Create a new Jupyter Notebook for this episode.

Start Docker If you have already successfully installed and run the Docker example with python tools, then you need only execute the following command.

docker start -i my_python  #give the name of your container

If this doesn’t work, return to the python tools Docker container lesson to work through how to start the container.

Clone a new repository

In your python Docker container clone the repository for this exercise and go into the cloned directory.

git clone https://github.com/cms-opendata-workshop/workshop2022-lesson-ttbarljetsanalysis-payload.git

cd workshop2022-lesson-ttbarljetsanalysis-payload

Launch Jupyter Lab In your docker python container, type the following.

jupyter-lab --ip=0.0.0.0 --no-browser

Take note of the last two lines that start with http://. Start up a browser locally on your laptop or desktop (not from the Docker container). Copy one of those URLs and paste it into the browser. If the first URL doesn’t work, try the other.

Start a new Jupyter notebook

The top icon (under Notebook) says Python 3 (ipykernel). Click on this icon. This should launch a new Jupyter notebook!

In this Jupyter Lab environment, click on File (in the top right) and then from the dropdown menu select Rename Notebook…. You can call this notebook whatever you like but I have called mine ttbar_analysis.ipynb.

For the remainder of this lesson, you’ll be typing or cutting-and-pasting the commands you see here in the Python sections into the Jupyter Notebook. To run those commands after you have typed them, you can press the little Play icon (right-pointing triangle) or type Shift + Enter (to run the cell and advance) or Ctrl + Enter (to run the cell and not advance). Whichever you prefer.

Optional! Using ipython

If, for some reason, you don’t want to use Jupyter, you can launch interactive python just by typing ipython in Docker Container (and not the jupyter-lab command) and then entering the python commands there.

The analysis

This episode is a recast of the analysis demo presented by Alexander Held at the IRIS-HEP AGC Workshop 2022. Our attempt is to make it more understandable by paying a bit more attention to the details. Note that this is work in progress and it will be refined in the future, perhaps using better consolidated ntuples (nanoAOD-like).

Datasets and pre-selection

As it was mentioned in the previous episode, we will be working towards a measurement of the top and anti-top quark production cross section \(\sigma_{t\bar{t}}\).
The \(t\bar{t}\) pair is identified in a particular decay mode referred to as the lepton+jets final state.

\[\begin{eqnarray} pp &\rightarrow& t\bar{t}\\ t\bar{t} &\rightarrow& (bW^{+})(\bar{b}W_{-}) \\ & & W^{+} \rightarrow q\bar{q} \\ & & W_{-} \rightarrow l^{-}\bar{\nu_{l}} \end{eqnarray}\]

Both top-quarks decay to a \(b\)-quark and a \(W\) boson. The \(b\)-quarks quickly hadronize, forming mesons which live long enough to travel hundreds of microns before decaying, allowing our algorithms to {\it tag} these jets as originating from \(b\)-quarks. This is known as b-tagging.

We then require that 1 of the \(W\) bosons decays to two quarks which manifest as 2 jets in the detector. We require that the other \(W\) boson decays to a charged lepton and a neutrino. \(\tau\) leptons decay rather quickly so we look for events where the charged lepton is an electron or neutrino. The neutrino is not detected but contributes to missing transverse energy.

So to summarize, our final state is characterized by one charged lepton (an electron or muon), significant missing transverse energy, and four jets, two of which are identified as b-jets.

\[t\bar{t} \rightarrow (bW^{+})(\bar{b}W_{-}) \rightarrow bq\bar{q} bl^{-}\bar{\nu_{l}}\]

Of course, this final state can be produced by other physics processes as well! To perform any analysis, we usually need the following:

The collision data (from the actual detector)
Simulated datasets (Monte Carlo or MC)
- Simulations of our signal process
- Simulations of our signal process, varied under certain assumptions to estimate systematic uncertainties
- Simulations of background process which could mimic the signal

For this analysis we will use the following datasets:

type	dataset	variation	CODP name	xsec [pb]	size (TB)	Rec ID
colisions data	data	nominal	/SingleMuon/Run2015D-16Dec2015-v1/MINIAOD		1.4	24119
			/SingleElectron/Run2015D-08Jun2016-v1/MINIAOD		2.6	24120
signal	ttbar	nominal	TT_TuneCUETP8M1_13TeV-powheg-pythia8	831.76	3.4	19980
		scaledown	TT_TuneCUETP8M1_13TeV-powheg-scaledown-pythia8		1.4	19983
		scaleup	TT_TuneCUETP8M1_13TeV-powheg-scaleup-pythia8		1.3	19985
		ME_var	TTJets_TuneCUETP8M1_13TeV-amcatnloFXFX-pythia8		1.3	19949
		PS_var	TT_TuneEE5C_13TeV-powheg-herwigpp		0.8	19999
backgrounds	single_top_t_chan	nominal	ST_t-channel_4f_leptonDecays_13TeV-amcatnlo-pythia8_TuneCUETP8M1	44.33	0.52	19397
	single_atop_t_chan	nominal	ST_t-channel_antitop_4f_leptonDecays_13TeV-powheg-pythia8_TuneCUETP8M1	26.38	0.042	19407
	single_top_tW	nominal	ST_tW_top_5f_inclusiveDecays_13TeV-powheg-pythia8_TuneCUETP8M1	35.6	0.03	19419
			ST_tW_antitop_5f_inclusiveDecays_13TeV-powheg-pythia8_TuneCUETP8M1	35.6	0.03	19412
	wjets	nominal	WJetsToLNu_TuneCUETP8M1_13TeV-amcatnloFXFX-pythia8	61526.7	3.8	20548

The nominal variation samples are the regular samples used in the analysis while samples corresonding to other variations are used for estimating systematic uncertainties. This will be discussed in the last episode.

As you can see, several of these datasets are quite large (TB in size), therefore we need to skim them. Also, as you were able to see previously, running CMSSW EDAnalyzers over these data (with the POET code, for instance) could be quite computing intensive. One could also estimate the time it would take to run over all the datasets we need using a single computer. To be efficient, you will need a computer cluster, but we will leave that for the Cloud Computing lesson.

Fortunately, we have prepared these skims already at CERN, using CERN/CMS computing infrastructure. The skimmed files we will be using were obtained in essentially the same POET way, except that we applied some trigger filtering and some pre-selection requirements.

We explicitly required:

That the events fired at least one of these triggers: HLT_Ele22_eta2p1_WPLoose_Gsf, HLT_IsoMu20_v, HLT_IsoTkMu20_v. We assume these triggers were unprescaled, but you know now, one should really check (or ask!)
- You might be able to infer from the names that these triggers are designed to record events with an electron (XXX_Ele_XXX) or a muon (XXX_Mu_XXX)
That the event contains either at least one tight electron with \(p_{T} > 26\) and \(\lvert\eta\rvert<2.1\) or at least one tight muon with \(p_{T} > 26\) and \(\lvert\eta\rvert<2.1\).
- When we use the word tight in this context, it is jargon internal to CMS that just specifies how pure we are trying to make the sample. A tight selection criteria would be quite pure and have fewer false positives than a medium or loose selection which might retain more ttrue muons or electrons, but also have more false postives.

A json file called ntuples.json was created in order to keep track of these files and their metadata. You can find this file in your copy of the workshop2022-lesson-ttbarljetsanalysis-payload repository.

Explore!

If you’d like to see what is in ntuples.json, you can use the file browser in Jupyter-lab, located on the left-hand side of the window.

First select workshop2022-lesson-ttbarljetsanalysis-payload/ and then ntuples.json. Click on the different names to expand them to see more information about how many files were used and how many events were in those files.

Challenge!

How many events were in the ttbar nominal sample?

Solution

20620375

Building the basic analysis selection

Here we will attempt to build the histogram of a physical observable by implementing the physics object selection requirements that were used by the CMS analysts, who performed this analysis back in 2015.

For understanding the basics of the analysis implementation, we will first attempt the analysis over just one collisions dataset (just one small file). Then, we will encapsulate our analysis in a Coffea processor and run it for all datasets: collisions (wich we will call just data), signal and background.

Here is a summary of the selection requirements used in the original CMS analysis:

Muon Selection

Exactly one muon

\(p_T\) > 30 GeV, \(\lvert\eta\rvert<2.1\), tight ID

relIso < 0.15 (corrected for pile-up contamination).

This means that the muon is fairly isolated from the jets, a good requirement since muons can also come from jets or even other proton-proton collisions…not the type of muon we want!

SIP3D < 4

SIP3D refers for the Significance on the Impact Parameter in 3D, which tells us how likely it is that the lepton came from the primary proton-proton interaction point, rather than some a different proton-proton collision.

Electron Selection

Exactly one electron

\(p_T\) > 30 GeV, \(\lvert\eta\rvert<2.1\), tight ID

SIP3D < 4

Jet Selection

Require at least one jet

Loose jet ID

\(p_T\) > 30 GeV, \(\lvert\eta\rvert<2.4\), Fall15_25nsV2

Jets identified as b-jets if CSV discriminator value > 0.8 (medium working point)

CSV refers to Combined Secondary Vertex, an algorithm used to identify \(b\)-jets that travel some distance from the interaction point. The algorith tries to combine some number of charged tracks and see if they originate from a point in space (a vertext) that is not the primary interaction point (a secondary vertex).

If for some reason you need to start over as you are following along, take into account that the file coffeaAnalysis_basics.py, in your copy of the exercise repository, contains all the relevant commands needed to complete the basic analysis part that is shown in this section.

OK, you should have your Jupyter notebook open in your Jupyter lab running in your Docker container! Type along (cut-and-paste from this episode) with me!

Let’start fresh, import the needed libraries and open an example file (we include some additional libraries that will be needed):

import uproot
import numpy as np
import awkward as ak
import hist
import matplotlib.pyplot as plt
import mplhep as hep
from coffea.nanoevents import NanoEventsFactory, BaseSchema
from agc_schema import AGCSchema

Now, let’s read in one file from our signal Monte Carlo sample that simulates the decay of our \(t\bar{t}\) pair. We’ll be using coffea to read everything in and using our AGCSchema.

events = NanoEventsFactory.from_root('root://eospublic.cern.ch//eos/opendata/cms/derived-data/POET/23-Jul-22/RunIIFall15MiniAODv2_TT_TuneCUETP8M1_13TeV-powheg-pythia8_flat/00EFE6B3-01FE-4FBF-ADCB-2921D5903E44_flat.root', schemaclass=AGCSchema, treepath='events').events()

We will apply the selection criteria and then make a meaningful histogram. Let’s divide the selection requirements into Objects selection and Event selection.

Objects selection

First, start by applying a \(p_{T}\) cut for the objects of interest, namely electrons, muons and jets. To compare, first check the number of objects in each subarray of the original collection:

print("Electrons:")
print(f"Number of events: {ak.num(events.electron, axis=0)}")
print(ak.num(events.electron, axis=1))
print()

print("Muons:")
print(f"Number of events: {ak.num(events.muon, axis=0)}")
print(ak.num(events.muon, axis=1))
print()

print("Jets:")
print(f"Number of events: {ak.num(events.jet, axis=0)}")
print(ak.num(events.jet, axis=1))

Check yourself!

Does this output make sense to you? Check with the instructor if it does not.

Before we go on, let’s do a quick check on the fields available for each of our objects of interest:

print("Electron fields:")
print(events.electron.fields)
print()

print("Muon fields:")
print(events.muon.fields)
print()

print("Jet fields:")
print(events.jet.fields)
print()

Now, let’s apply the \(p_{T}\) and \(\eta\) mask together with the tightness requirement for the leptons, along with our selection criteria for the jets. To remind ourselves…

Physics requirements

Muon

\(p_T\) > 30 GeV

\(\lvert\eta\rvert\) < 2.1

tight ID

relIso < 0.15 (corrected for pile-up contamination).

SIP3D < 4

Electron

Exactly one electron

\(p_T\) > 30 GeV

\(\lvert\eta\rvert\) < 2.1

tight ID

SIP3D < 4

Jet

Require at least one jet

Loose jet ID

\(p_T\) > 30 GeV

\(\lvert\eta\rvert\) < 2.4

Jets identified as b-jets if CSV discriminator value > 0.8 (medium working point)

selected_electrons = events.electron[(events.electron.pt > 30) & (abs(events.electron.eta)<2.1) & (events.electron.isTight == True)]

selected_muons = events.muon[(events.muon.pt > 30) & (abs(events.muon.eta)<2.1) & (events.muon.isTight == True)]

selected_jets = events.jet[(events.jet.corrpt > 30) & (abs(events.jet.eta)<2.4)]

Check yourself!

Can you match the python code to the physics selection criteria? Have we added all the requirements yet?

See what we got:

print("Selected objects ------------")

print("Electrons:")
print(f"Number of events: {ak.num(selected_electrons, axis=0)}")
print(ak.num(selected_electrons, axis=1))
print()

print("Muons:")
print(f"Number of events: {ak.num(selected_muons, axis=0)}")
print(ak.num(selected_muons, axis=1))
print()

print("Jets:")
print(f"Number of events: {ak.num(selected_jets, axis=0)}")
print(ak.num(selected_jets, axis=1))

Note that the number of events are still the same, for example:

print("Electrons before selection:")
print(f"Number of events: {ak.num(events.electron, axis=0)}")
print(ak.num(events.electron, axis=1))
print()

print("Electrons: after selection")
print(f"Number of events: {ak.num(selected_electrons, axis=0)}")
print(ak.num(selected_electrons, axis=1))
print()

Also, check one particular subarray to see if the applied requirements make sense:

print("pt before/after")
print(events.muon.pt[4])
print(selected_muons.pt[4])
print()

print("eta before/after")
print(events.muon.eta[4])
print(selected_muons.eta[4])
print()

print("isTight before/after")
print(events.muon.isTight[4])
print(selected_muons.isTight[4])

Challenge: Adding isolation and sip3d requirements for leptons

Please resist the urge to look at the solution. Only compare with the proposed solution after you make your own attempt.

Redo the lepton selection above (for selected_electrons, selected_muons) to include:

The relIsolation requirement for the muons (the one we built for dealing with pile-up)

The requirement for the Significance on the Impact Parameter in 3D (SIP3D) for muons and electrons
Solution
selected_electrons = events.electron[(events.electron.pt > 30) & (abs(events.electron.eta)<2.1) & (events.electron.isTight == True) & (events.electron.sip3d < 4)]
selected_muons = events.muon[(events.muon.pt > 30) & (abs(events.muon.eta)<2.1) & (events.muon.isTight == True) & (events.muon.sip3d < 4) & (events.muon.pfreliso04DBCorr < 0.15)]

Events selection

At this point it would be good to start playing around with the different methods that awkward gives you. Remember tha when exploring interactively, you could always type ak. and hit the Tab key to see the different methods available:

>>> ak.
Display all 123 possibilities? (y or n)
ak.Array(                  ak.awkward                 ak.from_arrow(             ak.kernels(                ak.operations              ak.strings_astype(         ak.types
ak.ArrayBuilder(           ak.behavior                ak.from_awkward0(          ak.layout                  ak.packed(                 ak.sum(                    ak.unflatten(
ak.ByteBehavior(           ak.behaviors               ak.from_buffers(           ak.linear_fit(             ak.pad_none(               ak.to_arrow(               ak.unzip(
ak.ByteStringBehavior(     ak.broadcast_arrays(       ak.from_categorical(       ak.local_index(            ak.parameters(             ak.to_arrow_table(         ak.validity_error(
ak.CategoricalBehavior(    ak.cartesian(              ak.from_cupy(              ak.mask(                   ak.partition               ak.to_awkward0(            ak.values_astype(
ak.CharBehavior(           ak.categories(             ak.from_iter(              ak.materialized(           ak.partitioned(            ak.to_buffers(             ak.var(
ak.Record(                 ak.combinations(           ak.from_jax(               ak.max(                    ak.partitions(             ak.to_categorical(         ak.virtual(
ak.Sized()                 ak.concatenate(            ak.from_json(              ak.mean(                   ak.prod(                   ak.to_cupy(                ak.where(
ak.StringBehavior(         ak.copy(                   ak.from_numpy(             ak.min(                    ak.ptp(                    ak.to_jax(                 ak.with_cache(
ak.all(                    ak.corr(                   ak.from_parquet(           ak.mixin_class(            ak.ravel(                  ak.to_json(                ak.with_field(
ak.any(                    ak.count(                  ak.from_regular(           ak.mixin_class_method(     ak.regularize_numpyarray(  ak.to_kernels(             ak.with_name(
ak.argcartesian(           ak.count_nonzero(          ak.full_like(              ak.moment(                 ak.repartition(            ak.to_layout(              ak.with_parameter(
ak.argcombinations(        ak.covar(                  ak.highlevel               ak.nan_to_num(             ak.run_lengths(            ak.to_list(                ak.without_parameters(
ak.argmax(                 ak.fields(                 ak.is_categorical(         ak.nplike                  ak.singletons(             ak.to_numpy(               ak.zeros_like(
ak.argmin(                 ak.fill_none(              ak.is_none(                ak.num(                    ak.size(                   ak.to_pandas(              ak.zip(
ak.argsort(                ak.firsts(                 ak.is_valid(               ak.numba                   ak.softmax(                ak.to_parquet(
ak.atleast_1d(             ak.flatten(                ak.isclose(                ak.numexpr                 ak.sort(                   ak.to_regular(
ak.autograd                ak.forms                   ak.jax                     ak.ones_like(              ak.std(                    ak.type(

You could also get some help on what they do by typing, in your interactive prompt, something like:

help(ak.count)

to obtain:

Help on function count in module awkward.operations.reducers:

count(array, axis=None, keepdims=False, mask_identity=False)
    Args:
        array: Data in which to count elements.
        axis (None or int): If None, combine all values from the array into
            a single scalar result; if an int, group by that axis: `0` is the
            outermost, `1` is the first level of nested lists, etc., and
            negative `axis` counts from the innermost: `-1` is the innermost,
            `-2` is the next level up, etc.
        keepdims (bool): If False, this reducer decreases the number of
            dimensions by 1; if True, the reduced values are wrapped in a new
            length-1 dimension so that the result of this operation may be
            broadcasted with the original array.
        mask_identity (bool): If True, reducing over empty lists results in
            None (an option type); otherwise, reducing over empty lists
            results in the operation's identity.

    Counts elements of `array` (many types supported, including all
    Awkward Arrays and Records). The identity of counting is `0` and it is
    usually not masked.

    This function has no analog in NumPy because counting values in a
    rectilinear array would only result in elements of the NumPy array's
    [shape](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.shape.html).

    However, for nested lists of variable dimension and missing values, the
    result of counting is non-trivial. For example, with this `array`,

        ak.Array([[ 0.1,  0.2      ],
                  [None, 10.2, None],
                  None,
                  [20.1, 20.2, 20.3],
                  [30.1, 30.2      ]])

    the result of counting over the innermost dimension is

        >>> ak.count(array, axis=-1)
        <Array [2, 1, None, 3, 2] type='5 * ?int64'>

    the outermost dimension is

        >>> ak.count(array, axis=0)
        <Array [3, 4, 1] type='3 * int64'>

    and all dimensions is

        >>> ak.count(array, axis=None)
        8

Let’s work on the single lepton requirement. Remember, the criteria indicates that we will only consider events with exactly one electron or exactly one muon. Let’see how we can do this:

event_filters = ((ak.count(selected_electrons.pt, axis=1) + ak.count(selected_muons.pt, axis=1)) == 1)

Note that the + between the two masks acts as an or! So we are requiring at exactly 1 electron or 1 muon.

In order to keep the analyisis regions (we will see this later) from the original AGC demo, let’s require at least four jets in our event filter:

event_filters = event_filters & (ak.count(selected_jets.corrpt, axis=1) >= 4)

We are adding to our event_filters requirements. The ampersand & means that we want both the previous definition of event_filters and the requirement of at least 4 jets.

Challenge: Require at least one b-tagged jet

Please resist the urge to look at the solution. Only compare with the proposed solution after you make your own attempt.

To the event_filters above, add the requirement to have at least one b-tagged jet with score above the proposed threshold (medium point; see above)
Solution
# at least one b-tagged jet ("tag" means score above threshold)
B_TAG_THRESHOLD = 0.8

event_filters = event_filters & (ak.sum(selected_jets.btag >= B_TAG_THRESHOLD, axis=1) >= 1)

Let’s now apply the event filters. We are applying the same event_filters mask to the events as well as the physics objects.

selected_events = events[event_filters]
selected_electrons = selected_electrons[event_filters]
selected_muons = selected_muons[event_filters]
selected_jets = selected_jets[event_filters]

Signal region selection

In a typical analysis one can construct a control region (with no essentially no expected signal) and a signal region (with signal events). Let’s call our signal region 4j2b, because the final state of the process we are aiming to measure has at least 4, two of which should be from b quarks.

Let’s define a filter for this region and create such region:

region_filter = ak.sum(selected_jets.btag > B_TAG_THRESHOLD, axis=1) >= 2

selected_jets_region = selected_jets[region_filter]

Now, here is where the true power of columnar analysis and the wonderful python tools that are being developed become really evident. Let’s reconstruct the hadronic top as the bjj system with the largest \(p_{T}\). We will get ourselves an observable, which is the mass.

# Use awkward to create all possible trijet candidates within events
trijet = ak.combinations(selected_jets_region, 3, fields=["j1", "j2", "j3"])

# Calculate four-momentum of tri-jet system. This is for all combinations
# Note that we are actually adding a `p4` field.
trijet["p4"] = trijet.j1 + trijet.j2 + trijet.j3 

# Pull out the b-tag of the jet with the maxium value (most likely to be a b-tag)
trijet["max_btag"] = np.maximum(trijet.j1.btag, np.maximum(trijet.j2.btag, trijet.j3.btag))

# Require at least one-btag in trijet candidates
trijet = trijet[trijet.max_btag > B_TAG_THRESHOLD]

# pick trijet candidate with largest pT and calculate mass of system
trijet_mass = trijet["p4"][ak.argmax(trijet.p4.pt, axis=1, keepdims=True)].mass

# Get the mass ready for plotting!
observable = ak.flatten(trijet_mass)

Challenge: Can you figure out what is happening above?

Take some time to understand the logic of the above statements and explore the awkward methods used to get the observable.

Histogramming and plotting

More information on this topic, including a very instructive video, can be found in one of the tutorials of the IRIS-HEP AGC Tools 2021 Workshop. We will not go into the details here, but just show you some examples.

We will use Hist from the hist package.

So, now we have a flat array for our observable. What else do we need for plotting? Well, a histogram is essentially a way to reduce our data. We can’t just plot every value of trijet mass, so we divide up our range of masses into n bins across some reasonable range. Thus, we need to define the mapping for our reduction; defining the number of bins and the range is sufficient for this. This is called a Regular axis in the hist.Hist package.

In our case, let’s plot 25 bins between values of 50 and 550. Because a histogram can contain an arbitrary amount of axes, we also need to give our axis a name (which becomes its reference in our code) and a label (which is the label on the axis that users see when the histogram is plotted).

Since we will be using several datasets (for signal, background and collisions data) we need a way of keeping these contributions separate in our histograms. One can do with this using Categorical axes. A Categorical axis takes a name, a label, and a pre-defined list of categories. Let’s book a generic histogram with such capabilities:

# This defines the histogram object, but doesn't actually fill it with the data.

histogram = hist.Hist.new.Reg(25, 50, 550,
                              name="observable", label="observable [GeV]")\
                             .StrCat(["4j1b", "4j2b"], name="region", label="Region")\
                             .StrCat([], name="process", label="Process", growth=True)\
                             .StrCat([], name="variation", label="Systematic variation", growth=True)\
                             .Weight()

This histogram placeholder is of type that can accep a Weight to the data tha goes in. This is because for simulated MC samples (backgrounds) , we will need to normalize the number of events to the total integrated luminosity.

By the way, if you look at the documentation,

help(hist.Hist.new)

you will find

|  Reg = Regular(self, bins: 'int', start: 'float', stop: 'float', *, name: 'str' = '', label: 'str' = '', metadata: 'Any' = None, flow: 'bool' = True, underflow: 'bool | None' = None, overflow: 'bool | None' 
= None, growth: 'bool' = False, circular: 'bool' = False, transform: 'AxisTransform | None' = None, __dict__: 'dict[str, Any] | None' = None) -> 'ConstructProxy'
 |  
 |  Regular(self, bins: 'int', start: 'float', stop: 'float', *, name: 'str' = '', label: 'str' = '', metadata: 'Any' = None, flow: 'bool' = True, underflow: 'bool | None' = None, overflow: 'bool | None' = None
, growth: 'bool' = False, circular: 'bool' = False, transform: 'AxisTransform | None' = None, __dict__: 'dict[str, Any] | None' = None) -> 'ConstructProxy'

It is useful at this point to do:

print(histogram.ndim)
print()

print(histogram.axes)

in order to understand the structure a bit better. You can see that this hist object is multidimensional holder for histograms, which makes it very convenient and very powerful. You could fill out the outter most StrCategories with several processes and variations. You can slice and dice. Here a very quick example: let’s say that, once the histogram is filled (we haven’t done that yet), you want to get the histograms which have to with the signal region. Accessing them is very simple:

histogram[:,1,:,:]

Now, let’s fill in the histogram:

histogram.fill(observable=observable, region="4j2b", process="ttbar", variation="nominal", weight=1)

and then plot

histogram[:,"4j2b","ttbar","nominal"].plot(histtype="fill", linewidth=1, edgecolor="grey", label='ttbar')
plt.legend()
plt.title(">= 4 jets, >= 2 b-tags")
plt.xlabel("$m_{bjj}$ [Gev]");
plt.show()

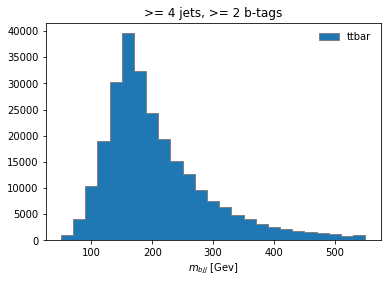
Coffea Processors

We now see how simple it could be to construct an analysis using python tools. Naturally, we would like to scale it up to a far larger datasets in any practical scenario. So the first expansion we can do to our analysis is to consider running it over more datasets, which include all of our data, our background, and the signal. Additionally, we would like to show to how to *estimate a few sources of systematic uncertainty, and for that we will be using, in some cases, additional datasets. These systematics datasets are generaly variations of the nominal ones.

To expand our analysis, we will use coffea Processors. Processors are coffea’s way of encapsulating an analysis in a way that is deployment-neutral. Once you have a Coffea analysis, you can throw it into a processor and use any of a variety of executors (e.g. Dask, Parsl, Spark) to chunk it up and run it across distributed workers. This makes scale-out simple and dynamic for users. Unfortunately, we don’t have the time to do such a demostration, but we will run it locally, with our vanilla coffea executor.

Key Point

If you ever get to use executors that can parallelize across distributed workers (e.g., Dask, Parsl, Spark), note that we can do this in HEP. Events are independent of each other, so if we split our work up and ship it off to different workers, we aren’t violating the data’s integrity. Furthermore, since the output we seek is a histogram, our output is also independent of how the work is split up. As long as each worker maps its data to a histogram, the summation of those histograms will be identical to a single worker processing all of the data. In coffea, an object that behaves in this way is called an accumulator.

Defining our coffea Processor

The processor includes a lot of the physics analysis details:

event filtering and the calculation of observables,
event weighting,
calculating systematic uncertainties at the event and object level,
filling all the information into histograms that get aggregated and ultimately returned to us by coffea

In the coffeaAnalysis_ttbarljets.py in your copy of the repository you will find the definition of our Processor. It is built as a python class, which nicely encapsulates it and, as advertised, becomes independent of the executor.

Inspect it briefly, you will recognize the basic ingredients that we already explored. The only difference is that it has been modified so it allows for additional features like running over different processes and/or variations of them and filling in corresponding histograms.

Take a look at the Processor implementation

Open the Processor

#------------------------------------
class TtbarAnalysis(processor_base):
#------------------------------------
    #--------------------
    def __init__(self):
    #--------------------
        num_bins = 25
        bin_low = 50
        bin_high = 550
        name = "observable"
        label = "observable [GeV]"
        #https://hist.readthedocs.io/en/latest/user-guide/quickstart.html
        #StrCat = StrCategory
        #https://hist.readthedocs.io/en/latest/banner_slides.html?highlight=StrCategory#many-axis-types
        self.hist = (
            hist.Hist.new.Reg(num_bins, bin_low, bin_high, name=name, label=label)
            .StrCat(["4j1b", "4j2b"], name="region", label="Region")
            .StrCat([], name="process", label="Process", growth=True)
            .StrCat([], name="variation", label="Systematic variation", growth=True)
            .Weight()
        )
    #-------------------------
    def process(self, events):
    #-------------------------
        histogram = self.hist.copy()

        process = events.metadata["process"]  # "ttbar" etc.
        variation = events.metadata["variation"]  # "nominal", "scaledown", etc.

        #print(f'Currently doing variation {variation} for {process}')

        # normalization for MC
        x_sec = events.metadata["xsec"]
        nevts_total = events.metadata["nevts"]
        # This truelumi number was obtained with
# brilcalc lumi -c web -i Cert_13TeV_16Dec2015ReReco_Collisions15_25ns_JSON_v2.txt -u /pb --normtag normtag_PHYSICS_2015.json  --begin 256630 --end 260627 > lumi2015D.txt
        # lumi in units of /pb
        lumi = 2256.38
        if process != "data":
            xsec_weight = x_sec * lumi / nevts_total
        else:
            xsec_weight = 1

        #### systematics
        # example of a simple flat weight variation, using the coffea nanoevents systematics feature
        # https://github.com/CoffeaTeam/coffea/blob/20a7e749eea3b8de4880088d2f0e43f6ef9d7993/coffea/nanoevents/methods/base.py#L84
        # Help on method add_systematic in module coffea.nanoevents.methods.base:
        # add_systematic(name: str, kind: str, what: Union[str, List[str], Tuple[str]], varying_function: Callable)
        # method of coffea.nanoevents.methods.base.NanoEventsArray instance
        if process == "wjets":
            events.add_systematic("scale_var", "UpDownSystematic", "weight", flat_variation)

        # example on how to get jet energy scale / resolution systematics
        # need to adjust schema to instead use coffea add_systematic feature, especially for ServiceX
        # cannot attach pT variations to events.jet, so attach to events directly
        # and subsequently scale pT by these scale factors
        events["pt_nominal"] = 1.0
        #events["pt_scale_up"] = 1.03
        # we have already these corrections in our data for this workshop, so we might as well use them
        # to assign a variation per jet and not per event. However, to avoid messing too much with this code, 
        # try a silly thing just for fun: take the average of jet variations per event (fill out the None values with a default 1.03)
        events['pt_scale_up'] = ak.fill_none(ak.mean(events.jet.corrptUp/events.jet.corrpt,axis=1),1.03)
        events["pt_res_up"] = jet_pt_resolution(events.jet.corrpt)

        pt_variations = ["pt_nominal", "pt_scale_up", "pt_res_up"] if variation == "nominal" else ["pt_nominal"]
        for pt_var in pt_variations:

            ### event selection
            # based on https://link.springer.com/article/10.1007/JHEP09(2017)051

            #object filters
            > > selected_electrons = events.electron[(events.electron.pt > 30) & (abs(events.electron.eta)<2.1) & (events.electron.isTight == True) & (events.electron.sip3d < 4)]
            > > selected_muons = events.muon[(events.muon.pt > 30) & (abs(events.muon.eta)<2.1) & (events.muon.isTight == True) & (events.muon.sip3d < 4) & (events.muon.pfreliso04DBCorr < 0.15)]
            jet_filter = (events.jet.corrpt * events[pt_var] > 30) & (abs(events.jet.eta)<2.4)
            selected_jets = events.jet[jet_filter]

            # single lepton requirement
            event_filters = ((ak.count(selected_electrons.pt, axis=1) + ak.count(selected_muons.pt, axis=1)) == 1)
            # at least four jets
            pt_var_modifier = events[pt_var] if "res" not in pt_var else events[pt_var][jet_filter]
            event_filters = event_filters & (ak.count(selected_jets.corrpt * pt_var_modifier, axis=1) >= 4)
            # at least one b-tagged jet ("tag" means score above threshold)
            B_TAG_THRESHOLD = 0.8
            event_filters = event_filters & (ak.sum(selected_jets.btag >= B_TAG_THRESHOLD, axis=1) >= 1)

            # apply event filters
            selected_events = events[event_filters]
            selected_electrons = selected_electrons[event_filters]
            selected_muons = selected_muons[event_filters]
            selected_jets = selected_jets[event_filters]

            for region in ["4j1b", "4j2b"]:
                # further filtering: 4j1b CR with single b-tag, 4j2b SR with two or more tags
                if region == "4j1b":
                    region_filter = ak.sum(selected_jets.btag >= B_TAG_THRESHOLD, axis=1) == 1
                    selected_jets_region = selected_jets[region_filter]
                    # use HT (scalar sum of jet pT) as observable
                    pt_var_modifier = events[event_filters][region_filter][pt_var] if "res" not in pt_var else events[pt_var][jet_filter][event_filters][region_filter]
                    observable = ak.sum(selected_jets_region.corrpt * pt_var_modifier, axis=-1)

                elif region == "4j2b":
                    region_filter = ak.sum(selected_jets.btag > B_TAG_THRESHOLD, axis=1) >= 2
                    selected_jets_region = selected_jets[region_filter]

                    # reconstruct hadronic top as bjj system with largest pT
                    # the jet energy scale / resolution effect is not propagated to this observable at the moment
                    trijet = ak.combinations(selected_jets_region, 3, fields=["j1", "j2", "j3"])  # trijet candidates
                    trijet["p4"] = trijet.j1 + trijet.j2 + trijet.j3  # calculate four-momentum of tri-jet system
                    trijet["max_btag"] = np.maximum(trijet.j1.btag, np.maximum(trijet.j2.btag, trijet.j3.btag))
                    trijet = trijet[trijet.max_btag > B_TAG_THRESHOLD]  # require at least one-btag in trijet candidates
                    # pick trijet candidate with largest pT and calculate mass of system
                    trijet_mass = trijet["p4"][ak.argmax(trijet.p4.pt, axis=1, keepdims=True)].mass
                    observable = ak.flatten(trijet_mass)

                ### histogram filling
                if pt_var == "pt_nominal":
                    # nominal pT, but including 2-point systematics
                    histogram.fill(
                            observable=observable, region=region, process=process, variation=variation, weight=xsec_weight
                        )


                    if variation == "nominal":
                        # also fill weight-based variations for all nominal samples
                        # this corresponds to the case for wjets included above as an example
                        for weight_name in events.systematics.fields:
                            for direction in ["up", "down"]:
                                # extract the weight variations and apply all event & region filters
                                weight_variation = events.systematics[weight_name][direction][f"weight_{weight_name}"][event_filters][region_filter]
                                # fill histograms
                                histogram.fill(
                                    observable=observable, region=region, process=process, variation=f"{weight_name}_{direction}", weight=xsec_weight*weight_variation
                                )

                        # calculate additional systematics: b-tagging variations
                        for i_var, weight_name in enumerate([f"btag_var_{i}" for i in range(4)]):
                            for i_dir, direction in enumerate(["up", "down"]):
                                # create systematic variations that depend on object properties (here: jet pT)
                                if len(observable):
                                    weight_variation = btag_weight_variation(i_var, selected_jets_region.corrpt)[:, i_dir]
                                else:
                                    weight_variation = 1 # no events selected
                                histogram.fill(
                                    observable=observable, region=region, process=process, variation=f"{weight_name}_{direction}", weight=xsec_weight*weight_variation
                                )

                elif variation == "nominal":
                    # pT variations for nominal samples
                    histogram.fill(
                            observable=observable, region=region, process=process, variation=pt_var, weight=xsec_weight
                        )
        output = {"nevents": {events.metadata["dataset"]: len(events)}, "hist": histogram}

        return output
    # https://coffeateam.github.io/coffea/api/coffea.processor.ProcessorABC.html?highlight=postprocess#coffea.processor.ProcessorABC.postprocess
    def postprocess(self, accumulator):
        return accumulator

Right below this Processor class, in the coffeaAnalysis_ttbarljets.py file, you will find a snippet which builds the input for the Processor (i.e., for the analysis):

# "Fileset" construction and metadata via utils.py file
# Here, we gather all the required information about the files we want to process: paths to the files and asociated metadata
# making use of the utils.py code in this repository
fileset = construct_fileset(N_FILES_MAX_PER_SAMPLE, use_xcache=False)
print(f"processes in fileset: {list(fileset.keys())}")
print(f"\nexample of information in fileset:\n { {\n  'files': [{fileset['ttbar__nominal']['files'][0]}, ...],")
print(f"  'metadata': {fileset['ttbar__nominal']['metadata']}\n } }")
t0 = time.time()

This is done with the help of the function construct_fileset, which is part of the utils.py file that you can also find in the repository. After you import the code in this file (like it is done in the heade of coffeaAnalysis_ttbarljets.py),

# Slimmed version of:
# https://github.com/iris-hep/analysis-grand-challenge/tree/main/analyses/cms-open-data-ttbar/utils
# These file contain code for bookkeeping and cosmetics, as well as some boilerplate
from utils import *

you get some utilities like styling routines and the fileset builder. Note that it is here where the cross sections for the different samples are stored. Also, the ntuples.json file (also find it in the repository) is read here to manage the fileset that will be fed to the Processor. We do some gymnastics also to adjust the normalization correctly. Finally there is a function to save the histograms in a ROOT file.

Next, in the coffeaAnalysis_ttbarljets.py file, you will see the call-out for the executor:

#Execute the data delivery pipeline
#we don't have an external executor, so we use local coffea (IterativeExecutor())
if PIPELINE == "coffea":
    executor = processor.IterativeExecutor()
    from coffea.nanoevents.schemas.schema import auto_schema
    schema = AGCSchema if PIPELINE == "coffea" else auto_schema
    run = processor.Runner(executor=executor, schema=schema, savemetrics=True, metadata_cache={})
    all_histograms, metrics = run(fileset, "events", processor_instance=TtbarAnalysis())
    all_histograms = all_histograms["hist"]

It is here where you decide where to run. Unfortunately, the datasets over which we are running are still quite large. So running on the whole dataset in a single computer is not very efficient. It will take a long time. Here is where coffea really performs, because you can ship it to different worker nodes using some different executors.

Finally note that there are some auxiliary functions at the beginning of the coffeaAnalysis_ttbarljets.py file and some histogramming routines at the end. We won’t worry about them for now.

Stop Jupyter Lab

We’re going to run a couple of commands now from the shell environment by calling some python scripts. So first, we need to save our work and shutdown Jupyter Lab.

Before saving our work, let’s stop the kernel and clear the output. That way we won’t save all the data and the notebook.

Click on Kernel and then Restart Kernel and Clear All Outputs.

Then, click on File and then Save Notebook.

Then, click on File and then Shut Down. You should now have your prompt back in the terminal with your Docker instance!

Running an example of the analysis

If you have a good connection you may get to run over just a single file per dataset by setting the N_FILES_MAX_PER_SAMPLE = 1 at the beggining of the coffeaAnalysis_ttbarljets.py file. Otherwise, do not worry we will provide you with the final histograms.root output after we ran over the whole dataset (for reference, it takes about 4 hours in a regular laptop).

If you have time! (probably not right now)

Edit coffeaAnalysis_ttbarljets.py so that N_FILES_MAX_PER_SAMPLE = 1 rather than N_FILES_MAX_PER_SAMPLE = -1. And then run the demonstrator:
cd /code/workshop2022-lesson-ttbarljetsanalysis-payload

python coffeaAnalysis_ttbarljets.py
This can take quite some time, even running over 1 file in each dataset, so you may want to do this on your own time and not during the synchronous parts of this workshop.

Plotting

Plotting the final results

Here you can download a full histograms.root. It was obtained after 4 hours of running on a single computer. When you click on the link, you’ll be directed to CERNBox, a tool to share large files, similar to DropBox.

To download the file, click on the three (3) vertical dots by the histograms.root name in the tab near the top. Then select Download.

When the file is downloaded, move it to to your cms_open_data_python/workshop2022-lesson-ttbarljetsanalysis-payload on your local laptop. Because this directory is mounted in your Docker container, you will be able to see this file in Docker.

Of course, if you have some available space, you could download the files (the size is not terribly large, maybe around 60GB or so), and run much faster. It contains all the histograms produced by the analysis Processor. We have prepared a plotting script for you to see the results:
python plotme.py

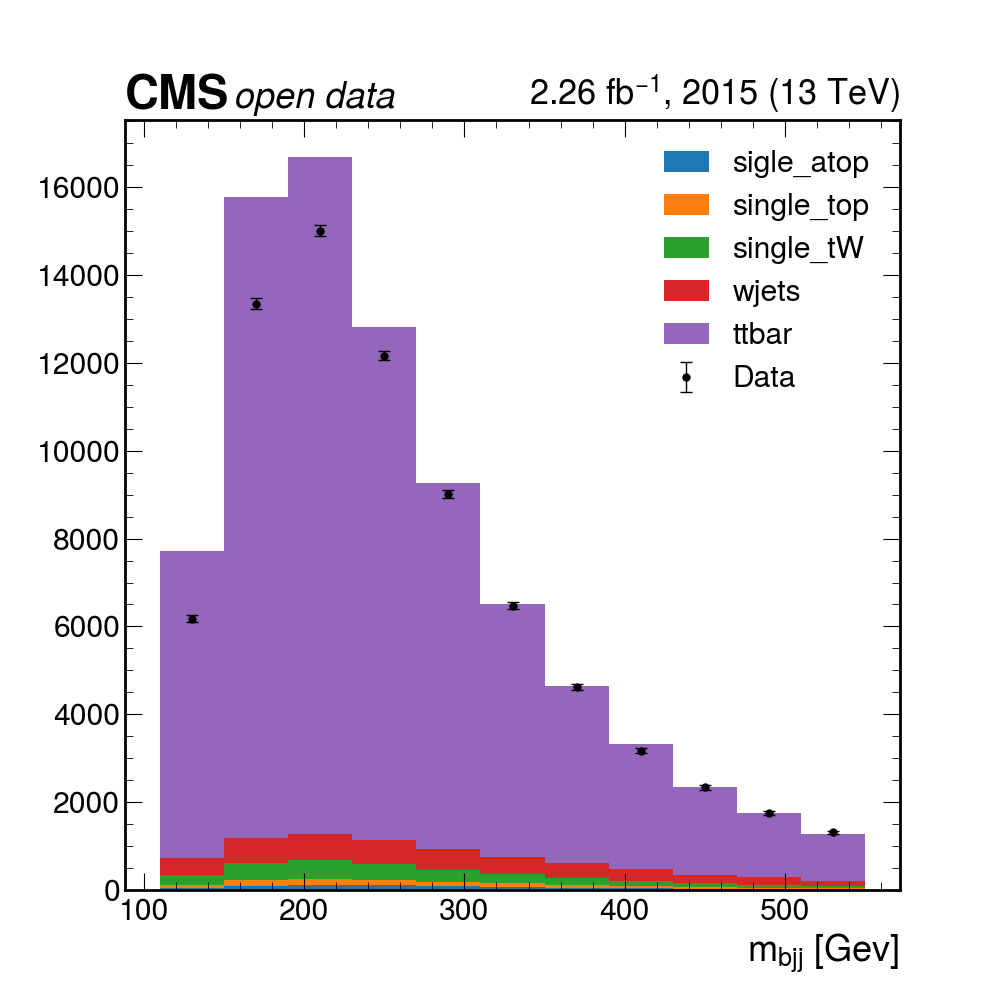
Pretty good! The data mostly seems to match up with our assumptions about how much the different MC samples contribute, but maybe we can do better if we allow for the fact that we may not know these values exactly. In the next section, we’ll try to use some inference tools to get a more precise description of the data!

Key Points

Basic selection requirements are implemented very easily using columnar analysis

Coffea processors encapsulate an analysis so it becomes deployment-neutral

previous episode

Simplified Run 2 Analysis

next episode

Coffea Analysis

Overview

Getting things prepared for this episode

Type out the following commands for this episode!

Optional! Using ipython

The analysis

Datasets and pre-selection

Explore!

Challenge!

Solution

Building the basic analysis selection

Muon Selection

Electron Selection

Jet Selection

Objects selection

Check yourself!

Physics requirements

Check yourself!

Challenge: Adding isolation and sip3d requirements for leptons

Solution

Events selection

Challenge: Require at least one b-tagged jet

Solution

Signal region selection

Challenge: Can you figure out what is happening above?

Histogramming and plotting

Coffea Processors

Key Point

Defining our coffea Processor

Take a look at the Processor implementation

Open the Processor

Stop Jupyter Lab

Running an example of the analysis

If you have time! (probably not right now)

Plotting

Plotting the final results

Key Points

previous episode

next episode