Analysis introduction

Overview

Teaching: 20 min
Exercises: 20 min

Questions

• What analysis will we be doing?

• What is columnar analysis?

Objectives

• Learn about the physics behind the analysis example.

• Learn about the strategy we will follow for our analysis example.

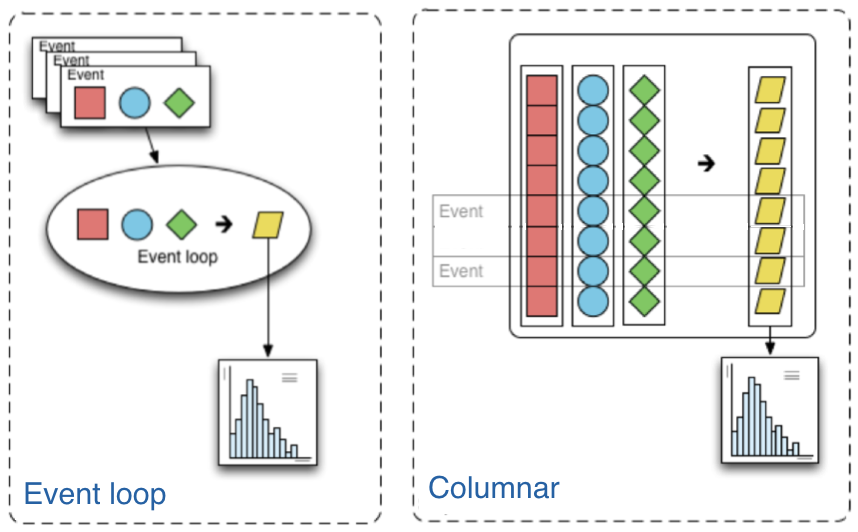
• Learn what the difference is between columnar and loop analysis.

Physics introduction

In this lesson, you will be walked through a mini-reproduction of a 2017 analysis from the CMS collaboration. The cross-section for the production of top-quark / anti-top-quark pairs in proton-proton collisions was measured. Put another way, we measured the probability that a top-quark and an anti-top quark pair are produced when protons are collided at a center-of-mass energy of 13 TeV.

.

To go into a bit more detail in this simplified analysis we will be working towards a measurement of the top and anti-top quark production cross section \(\sigma_{t\bar{t}}\). The data are produced in proton-proton collisions at \(\sqrt{s}\) = 13 TeV at the beginning of Run 2 of the LHC. We will be examining the lepton+jets final state \(t\bar{t} \rightarrow (bW^{+})(\bar{b}W_{-}) \rightarrow bq\bar{q} bl^{-}\bar{\nu_{l}}\) which is characterized by one lepton (here we look at electrons and muons only), significant missing transverse energy, and four jets, two of which are identified as b-jets.

During the live WHEPP workshop this session will focus on equipping you to analyze a POET ROOT file in python and make a basic plot of a kinematic quantity. Follow the ``Bonus Material” episodes to incorporate multiple simulated samples and apply the analysis selection criteria discussed in the Event Selection lesson!

Slides

We want to motivate why we are encouraging you to look into some of these newer software tools. By now, you should have heard about this particular measurement and how CMS reconstructs the different physics objects. If you’d like, you can review that material with these slides.

Together, we will go through these slides to get a more complete overview of what goes into an analysis and to understand why we need all these tools and how they make our life easier.

Launch Jupyter notebook

In your docker python container, type the following.

jupyter-lab --ip=0.0.0.0 --no-browser

Start a new Jupyter notebook

The top icon (under Notebook) says Python 3 (ipykernel). Click on this icon. This should launch a new Jupyter notebook!

Starting a new Jupyter notebook

If your new Jupyter Notebook started, you’ll see something like this.

In this Jupyter Lab environment, click on File (in the top right) and then from the dropdown menu select Rename Notebook…. You can call this notebook whatever you like but I have called mine analysis_example_prelesson.ipynb.

For the remainder of this lesson, you’ll be typing or cutting-and-pasting the commands you see here in the Python sections into the Jupyter Notebook. To run those commands after you have typed them, you can press the little Play icon (right-pointing triangle) or type Shift + Enter (to run the cell and advance) or Ctrl + Enter (to run the cell and not advance). Whichever you prefer.

Optional! Using ipython

If, for some reason, you don’t want to use Jupyter, you can launch interactive python just by typing ipython in Docker Container (and not the jupyter-lab command) and then entering the python commands there.

Columnar analysis basics with Awkward

Note: this and the next section on this episode are a recast (with some shameless copying and pasting) of this notebook by Mat Adamec presented during the IRIS-HEP AGC Workshop 2022.

In one of the pre-exercises we learned how to access ROOT files (the standard use at the LHC experiments) using uproot and why the awkward library can be very helpful when dealing with jagged arrays.

Opening and exploring a POET file

Let’s remember very quickly. First, be sure to import the appropriate libraries:

import uproot
import awkward as ak

Let’s open an example file. These are flattened POET ROOT files, in which the TTree objects for each individual physics object have been merged into one tree. We have produced these files for you!

Using uproot,

events = uproot.open('root://eospublic.cern.ch//eos/opendata/cms/upload/od-workshop/ws2021/myoutput_odws2022-ttbaljets-prodv2.0_merged.root')['events']
events

<TTree 'events' (275 branches) at 0x7fb46a8b5870>.

We now have an events tree. We can view its branches by querying its keys():

events.keys()

['numberelectron', 'nelectron_e', 'electron_e', 'nelectron_pt', 'electron_pt', 'nelectron_px', 'electron_px', 'nelectron_py', 'electron_py', 'nelectron_pz', 'electron_pz', 'nelectron_eta', 'electron_eta', 'nelectron_phi', 'electron_phi', 'nelectron_ch', 'electron_ch', 'nelectron_iso', 'electron_iso', 'nelectron_veto', 'electron_veto', 'nelectron_isLoose', 'electron_isLoose', 'nelectron_isMedium', 'electron_isMedium', 'nelectron_isTight', 'electron_isTight', 'nelectron_dxy', 'electron_dxy', 'nelectron_dz', 'electron_dz', 'nelectron_dxyError', 'electron_dxyError', 'nelectron_dzError', 'electron_dzError', 'nelectron_ismvaLoose', 'electron_ismvaLoose', 'nelectron_ismvaTight', 'electron_ismvaTight', 'nelectron_ip3d', 'electron_ip3d', 'nelectron_sip3d', 'electron_sip3d', 'numberfatjet', 'nfatjet_e', 'fatjet_e', 'nfatjet_pt', 'fatjet_pt', 'nfatjet_eta', 'fatjet_eta', 'nfatjet_phi', 'fatjet_phi', 'nfatjet_ch', 'fatjet_ch', 'nfatjet_mass', 'fatjet_mass', 'nfatjet_corrpt', 'fatjet_corrpt', 'nfatjet_corrptUp', 'fatjet_corrptUp', 'nfatjet_corrptDown', 'fatjet_corrptDown', 'nfatjet_corrptSmearUp', 'fatjet_corrptSmearUp', 'nfatjet_corrptSmearDown', 'fatjet_corrptSmearDown', 'nfatjet_corrmass', 'fatjet_corrmass', 'nfatjet_corre', 'fatjet_corre', 'nfatjet_corrpx', 'fatjet_corrpx', 'nfatjet_corrpy', 'fatjet_corrpy', 'nfatjet_corrpz', 'fatjet_corrpz', 'nfatjet_prunedmass', 'fatjet_prunedmass', 'nfatjet_softdropmass', 'fatjet_softdropmass', 'nfatjet_tau1', 'fatjet_tau1', 'nfatjet_tau2', 'fatjet_tau2', 'nfatjet_tau3', 'fatjet_tau3', 'nfatjet_subjet1btag', 'fatjet_subjet1btag', 'nfatjet_subjet2btag', 'fatjet_subjet2btag', 'nfatjet_subjet1hflav', 'fatjet_subjet1hflav', 'nfatjet_subjet2hflav', 'fatjet_subjet2hflav', 'numberjet', 'njet_e', 'jet_e', 'njet_pt', 'jet_pt', 'njet_eta', 'jet_eta', 'njet_phi', 'jet_phi', 'njet_ch', 'jet_ch', 'njet_mass', 'jet_mass', 'njet_btag', 'jet_btag', 'njet_hflav', 'jet_hflav', 'njet_corrpt', 'jet_corrpt', 'njet_corrptUp', 'jet_corrptUp', 'njet_corrptDown', 'jet_corrptDown', 'njet_corrptSmearUp', 'jet_corrptSmearUp', 'njet_corrptSmearDown', 'jet_corrptSmearDown', 'njet_corrmass', 'jet_corrmass', 'njet_corre', 'jet_corre', 'njet_corrpx', 'jet_corrpx', 'njet_corrpy', 'jet_corrpy', 'njet_corrpz', 'jet_corrpz', 'btag_Weight', 'btag_WeightUp', 'btag_WeightDn', 'met_e', 'met_pt', 'met_px', 'met_py', 'met_phi', 'met_significance', 'met_rawpt', 'met_rawphi', 'met_rawe', 'numbermuon', 'nmuon_e', 'muon_e', 'nmuon_pt', 'muon_pt', 'nmuon_px', 'muon_px', 'nmuon_py', 'muon_py', 'nmuon_pz', 'muon_pz', 'nmuon_eta', 'muon_eta', 'nmuon_phi', 'muon_phi', 'nmuon_ch', 'muon_ch', 'nmuon_isLoose', 'muon_isLoose', 'nmuon_isMedium', 'muon_isMedium', 'nmuon_isTight', 'muon_isTight', 'nmuon_isSoft', 'muon_isSoft', 'nmuon_isHighPt', 'muon_isHighPt', 'nmuon_dxy', 'muon_dxy', 'nmuon_dz', 'muon_dz', 'nmuon_dxyError', 'muon_dxyError', 'nmuon_dzError', 'muon_dzError', 'nmuon_pfreliso03all', 'muon_pfreliso03all', 'nmuon_pfreliso04all', 'muon_pfreliso04all', 'nmuon_pfreliso04DBCorr', 'muon_pfreliso04DBCorr', 'nmuon_TkIso03', 'muon_TkIso03', 'nmuon_jetidx', 'muon_jetidx', 'nmuon_genpartidx', 'muon_genpartidx', 'nmuon_ip3d', 'muon_ip3d', 'nmuon_sip3d', 'muon_sip3d', 'numberphoton', 'nphoton_e', 'photon_e', 'nphoton_pt', 'photon_pt', 'nphoton_px', 'photon_px', 'nphoton_py', 'photon_py', 'nphoton_pz', 'photon_pz', 'nphoton_eta', 'photon_eta', 'nphoton_phi', 'photon_phi', 'nphoton_ch', 'photon_ch', 'nphoton_chIso', 'photon_chIso', 'nphoton_nhIso', 'photon_nhIso', 'nphoton_phIso', 'photon_phIso', 'nphoton_isLoose', 'photon_isLoose', 'nphoton_isMedium', 'photon_isMedium', 'nphoton_isTight', 'photon_isTight', 'nPV_chi2', 'PV_chi2', 'nPV_ndof', 'PV_ndof', 'PV_npvs', 'PV_npvsGood', 'nPV_x', 'PV_x', 'nPV_y', 'PV_y', 'nPV_z', 'PV_z', 'trig_Ele22_eta2p1_WPLoose_Gsf', 'trig_IsoMu20', 'trig_IsoTkMu20', 'numbertau', 'ntau_e', 'tau_e', 'ntau_pt', 'tau_pt', 'ntau_px', 'tau_px', 'ntau_py', 'tau_py', 'ntau_pz', 'tau_pz', 'ntau_eta', 'tau_eta', 'ntau_phi', 'tau_phi', 'ntau_ch', 'tau_ch', 'ntau_mass', 'tau_mass', 'ntau_decaymode', 'tau_decaymode', 'ntau_iddecaymode', 'tau_iddecaymode', 'ntau_idisoraw', 'tau_idisoraw', 'ntau_idisovloose', 'tau_idisovloose', 'ntau_idisoloose', 'tau_idisoloose', 'ntau_idisomedium', 'tau_idisomedium', 'ntau_idisotight', 'tau_idisotight', 'ntau_idantieletight', 'tau_idantieletight', 'ntau_idantimutight', 'tau_idantimutight']

Each of these branches can be interpreted as an awkward array. Let’s examine their contents to remember that they contain jagged (non-rectangular) arrays:

muon_pt = events['muon_pt'].array()
print(muon_pt)

[[53.4, 0.792], [30.1], [32.9, 0.769, 0.766], ... 40], [37.9], [35.2], [30.9, 3.59]]

We could get the number of muons in each collision with:

ak.num(muon_pt, axis=-1)

<Array [2, 1, 3, 1, 1, 1, ... 1, 1, 1, 1, 1, 2] type='15090 * int64'>

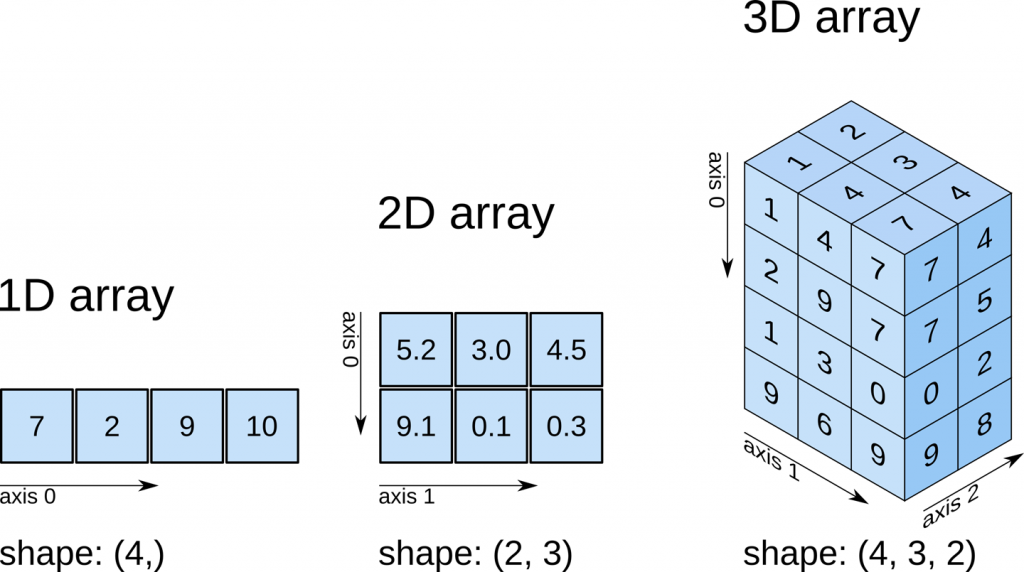
A quick note about axes in awkward: 0 is always the shallowest, while -1 is the deepest. In other words, axis=0 would tell us the number of subarrays (events), while axis=-1 would tell us the number of muons within each subarray. This array is only of dimension 2, so axis=1 or axis=-1 are the same. This usage is the same as for standard numpy arrays.

Applying masks

The traditional way of analyzing data in HEP involves the event loop. In this paradigm, we would write an explicit loop to go through every event (and through every field of an event that we wish to make a cut on). This method of analysis is rather bulky in comparison to the columnar approach, which (ideally) has no explicit loops at all! Instead, the fields of our data are treated as arrays and analysis is done by way of numpy-like array operations.

Most simple cuts can be handled by masking. A mask is a Boolean array which is generated by applying a condition to a data array. For example, if we want only muons with pT > 10, our mask would be:

print(muon_pt > 10)

[[True, False], [True], [True, False, False], ... [True], [True], [True, False]]

Then, we can apply the mask to our data. The syntax follows other standard array selection operations: data[mask]. This will pick out only the elements of our data which correspond to a True.

Our mask in this case must have the same shape as our muons branch, and this is guaranteed to be the case since it is generated from the data in that branch. When we apply this mask, the output should have the same amount of events, but it should down-select muons - muons which correspond to False should be dropped. Let’s compare to check:

print('Input:', muon_pt)
print('Output:', muon_pt[muon_pt > 10])

Input: [[53.4, 0.792], [30.1], [32.9, 0.769, 0.766], ... 40], [37.9], [35.2], [30.9, 3.59]]
Output: [[53.4], [30.1], [32.9], [28.3], [41.7], ... [42.6], [40], [37.9], [35.2], [30.9]]

We can also confirm we have fewer muons now, but the same amount of events:

print('Input Counts:', ak.sum(ak.num(muon_pt, axis=1)))
print('Output Counts:', ak.sum(ak.num(muon_pt[muon_pt > 10], axis=1)))

print('Input Size:', ak.num(muon_pt, axis=0))
print('Output Size:', ak.num(muon_pt[muon_pt > 10], axis=0))

Input Counts: 26690
Output Counts: 17274

Input Size: 15090
Output Size: 15090

Challenge!

How many muons have a transverse momentum (pt) greater than 30 GeV/c?

Revisit the output of event.keys(). How many jets in total were produced and how many have a transverse momentum greater than 30 GeV/c?

Solution

We modify the above code to mask the muons with muon_pt > 30. We also make use of the jet_pt variable to perform a similar calculation.

print('Input Counts:', ak.sum(ak.num(muon_pt, axis=1)))
print('Output Counts:', ak.sum(ak.num(muon_pt[muon_pt > 30], axis=1)))

Input Counts: 26690
Output Counts: 13061

jet_pt = events['jet_pt'].array()

print('Input Counts:', ak.sum(ak.num(jet_pt, axis=1)))
print('Output Counts:', ak.sum(ak.num(jet_pt[jet_pt > 30], axis=1)))

print('Input Counts:', ak.num(jet_pt, axis=0))
print('Output Counts:', ak.num(jet_pt[jet_pt > 30], axis=0))

Input Counts: 26472
Output Counts: 19419
Input Counts: 15090
Output Counts: 15090

So we find that there are 13061 muons, taken from these 15090 proton-proton collisions that have transverse momentum greater than 30 GeV/c.

Similarly we find that there are 26472 jets, taken from these 15090 proton-proton collisions, and 19419 of them have transverse momentum greater than 30 GeV/c.

Let’s quickly make a simple histogram with the widely used matplotlib library. First we will import it.

import matplotlib.pylab as plt

When we make our histogram, we need to first “flatten” the awkward aray before passing it to matplotlib. This is because matplotlib doesn’t know how to handle the jagged nature of awkward arrays.

# Flatten the jagged array before we histogram it
values = ak.flatten(events['jet_eta'].array())

fig = plt.figure(figsize=(6,4))
plt.hist(values,bins=100,range=(-5,5))
plt.xlabel(f'Jet $\eta$',fontsize=14)
;

(The semi-colon at the end of the code is just to suppress the output of whatever the last line of the python code in the cell.)

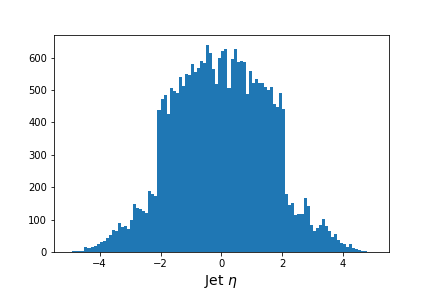
Output of jet_eta histogram

And here’s how we could use the mask in our plot.

# Flatten the jagged array before we histogram it
fig = plt.figure(figsize=(6,4))

values = ak.flatten(jet_pt)

plt.hist(values,bins=100,range=(0,100), label='All jets')
plt.hist(values[values>30],bins=100,range=(0,100), label='jets with pt>30 GeV/c')

plt.xlabel(f'Jet $p_T$',fontsize=14)
plt.legend()
;

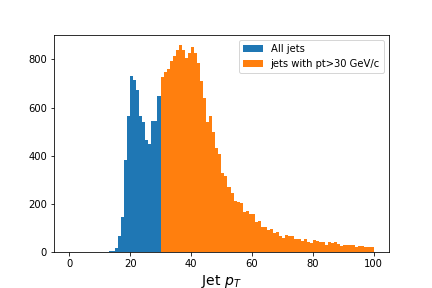
Output of jet_pt histogram with and without mask

Key Points

• Understanding the basic physics will help you understand how to translate physics into computer code.

• We will be perfoming a real but simplified HEP analysis using CMS Run2 open data using columnar analysis.