Content from Intro to CMS Physics Objects
Last updated on 2024-07-09 | Edit this page
Overview
Questions
- What do we call physics objects in CMS?
- How are physics objects reconstructed?
- How are physics objects represented in NanoAOD?
Objectives
- Learn about the different physics objects in CMS and get briefed on their reconstruction
- Learn more about the collection structure of NanoAOD
Overview
The CMS experment is a giant detector that acts like a camera that “photographs” particle collisions, allowing us to interpret their nature.
Certainly, we cannot directly observe all the particles created in the collisions because some of them decay very quickly or simply do not interact with our detector. However, we can infer their presence. If they decay to other stable particles and interact with the apparatus, they leave signals in the CMS subdetectors. These signals are used to reconstruct the decay products or infer their presence; we call these, physics objects.
Physics objects are built with the information collected by the sensors of the CMS detector. Take a look at the CMS experiment in the image below. This is a good recent video that you can watch later to get a quick feeling of how CMS looks now in Run 3.
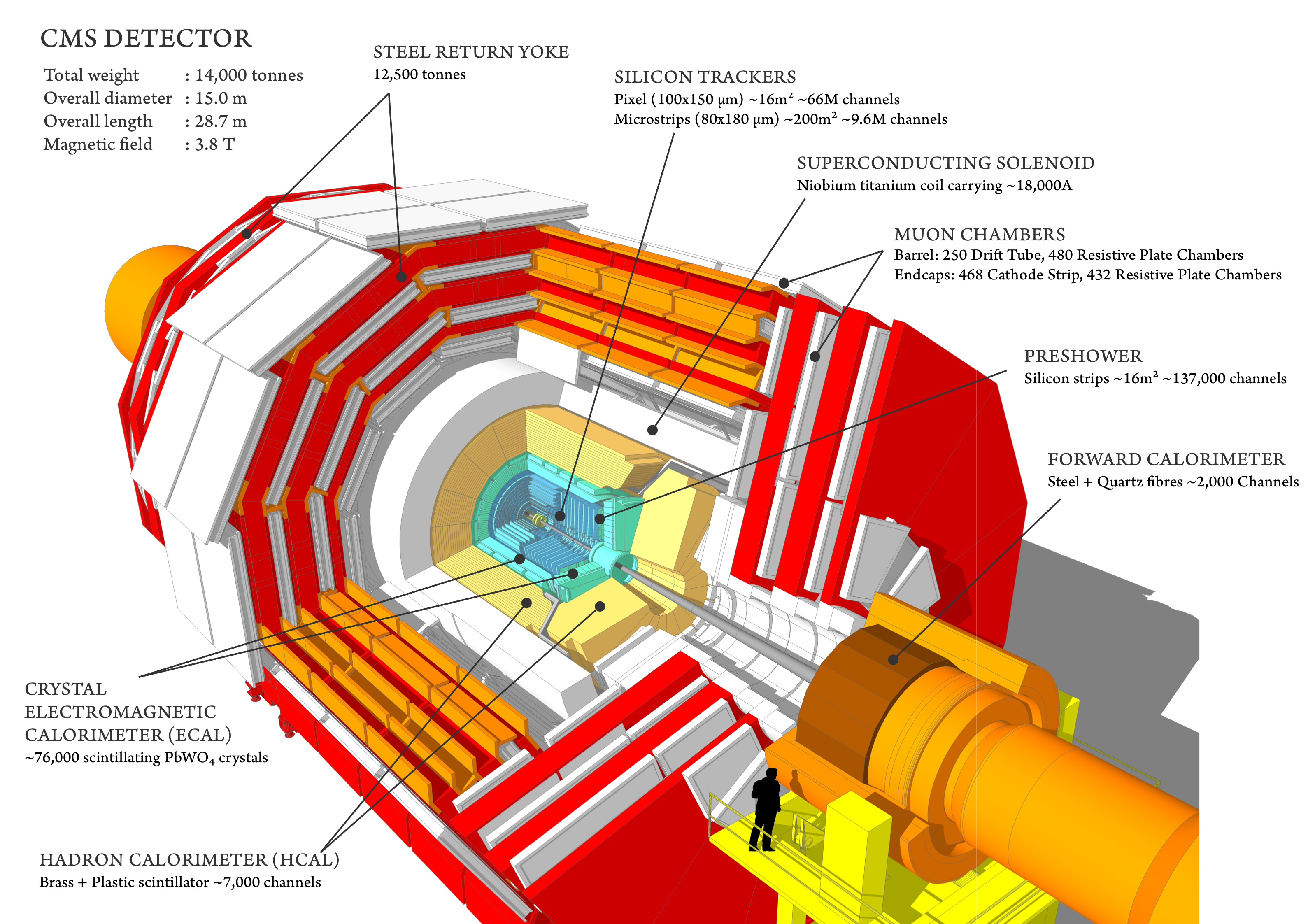
Physics objects could be
- muons
- electrons
- jets
- photons
- taus
- missing transverse momentum
In the CERN Open Portal (CODP) site one can find a more detailed description of these physical objects and a list of them corresponding to 2010, 2011/2012, and 2015/2016 releases of open data.
In this workshop we will focus on working with open data from the latest 2016 release from Run 2. This release included the NanoAOD file format that contains the most commonly used physics object information in a standard ROOT tree.
Physics Objects reconstruction
Physics objects are mainly reconstructed using methods like clustering and linking parts of a CMS subsystem to parts of other CMS subsystems. For instance, electromagnetic objects (electrons or photons) are reconstructed by the linking of tracks with ECAL energy deposits.
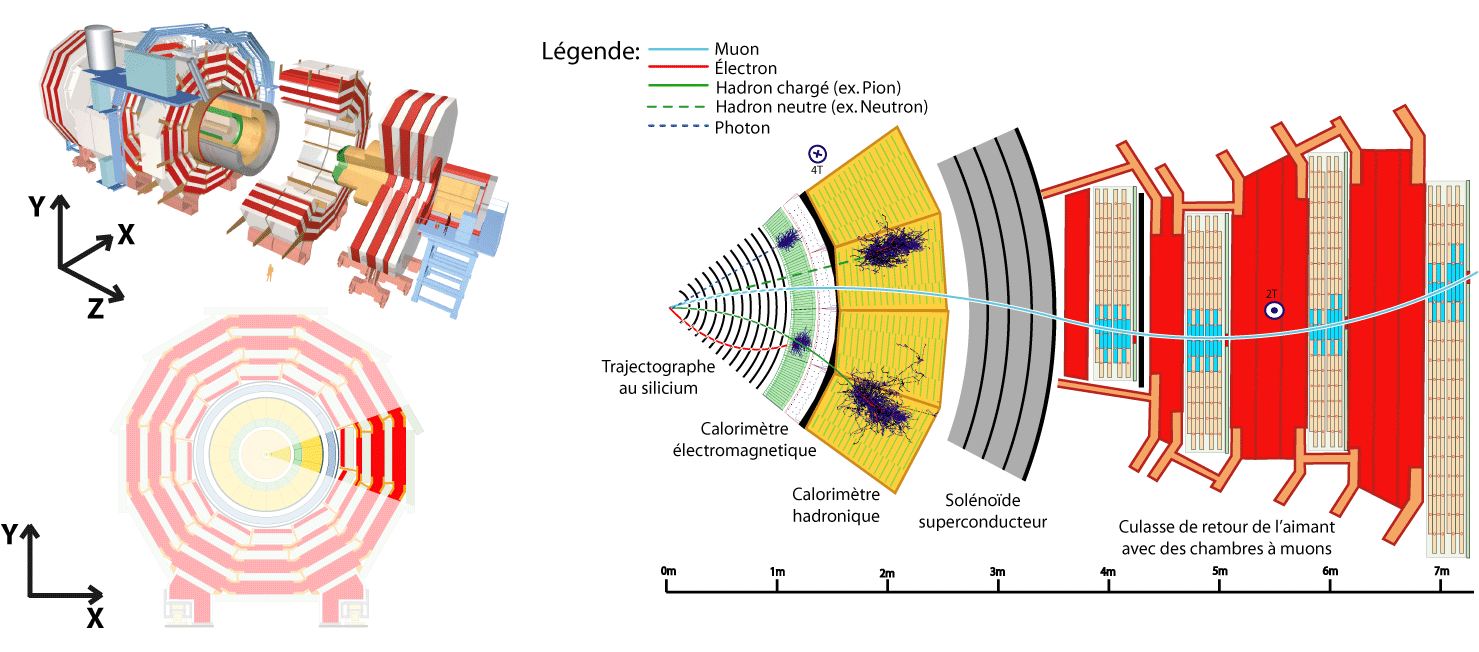
These actions are essential parts of the so-called Particle Flow (PF) algorithm.

The particle-flow (PF) algorithm aims at reconstructing and identifying all stable particles in the event, i.e., electrons, muons, photons, charged hadrons and neutral hadrons, with a thorough combination of all CMS sub-detectors towards an optimal determination of their direction, energy and type. This list of individual particles is then used, as if it came from a Monte-Carlo event generator, to build jets (from which the quark and gluon energies and directions are inferred), to determine the missing transverse energy (which gives an estimate of the direction and energy of the neutrinos and other invisible particles), to reconstruct and identify taus from their decay products and more.
The PF algorithm and all its reconstruction tributaries are written in C++ and are part of the CMSSW software that is required to analyze any open data in the earlier AOD or MiniAOD formats. For more information about the PF algorithm you can visit a lesson from an earlier workshop: Advanced Tools lesson. The CMS open data from 2016 contains some data samples in the NanoAOD format that have been supplemented with particle flow information: nanoad-pf samples.
Key Points
- Physics objects are the final abstraction in the detector that can be associated to physical entities like particles.
- NanoAOD stores physics object properties as branches of a ROOT tree, linked by common name prefixes.
Content from Electrons & Photons
Last updated on 2024-07-09 | Edit this page
Overview
Questions
- What are electromagnetic objects
- How are electrons treated in CMS?
- What variables are available in NanoAOD?
Objectives
- Understand what electromagnetic objects are in CMS
- Learn electron member functions for common track-based quantities
- Learn variables for identification and isolation of electrons
- Learn variables for electron detector-related quantities
Motivation
In the middle of the workshop we will be working on the main activity, which is to attempt to replicate a CMS physics analysis in a simplified way using modern analysis tools. The final state that we will be looking at contains electrons, muons and jets. We are using these objects as examples to review the way in which we extract physics objects information.
The analysis requires some special variables, which we will need to identify in our Open Data NanoAOD files.
Electromagnetic objects
We call photons and electrons electromagnetic particles because they leave most of their energy in the electromagnetic calorimeter (ECAL) so they share many common properties and functions
Many of the different hypothetical exotic particles are unstable and can transform, or decay, into electrons, photons, or both. Electrons and photons are also standard tools to measure better and understand the properties of already known particles. For example, one way to find a Higgs Boson is by looking for signs of two photons, or four electrons in the debris of high energy collisions. Because electrons and photons are crucial in so many different scenarios, the physicists in the CMS collaboration make sure to do their best to reconstruct and identify these objects.
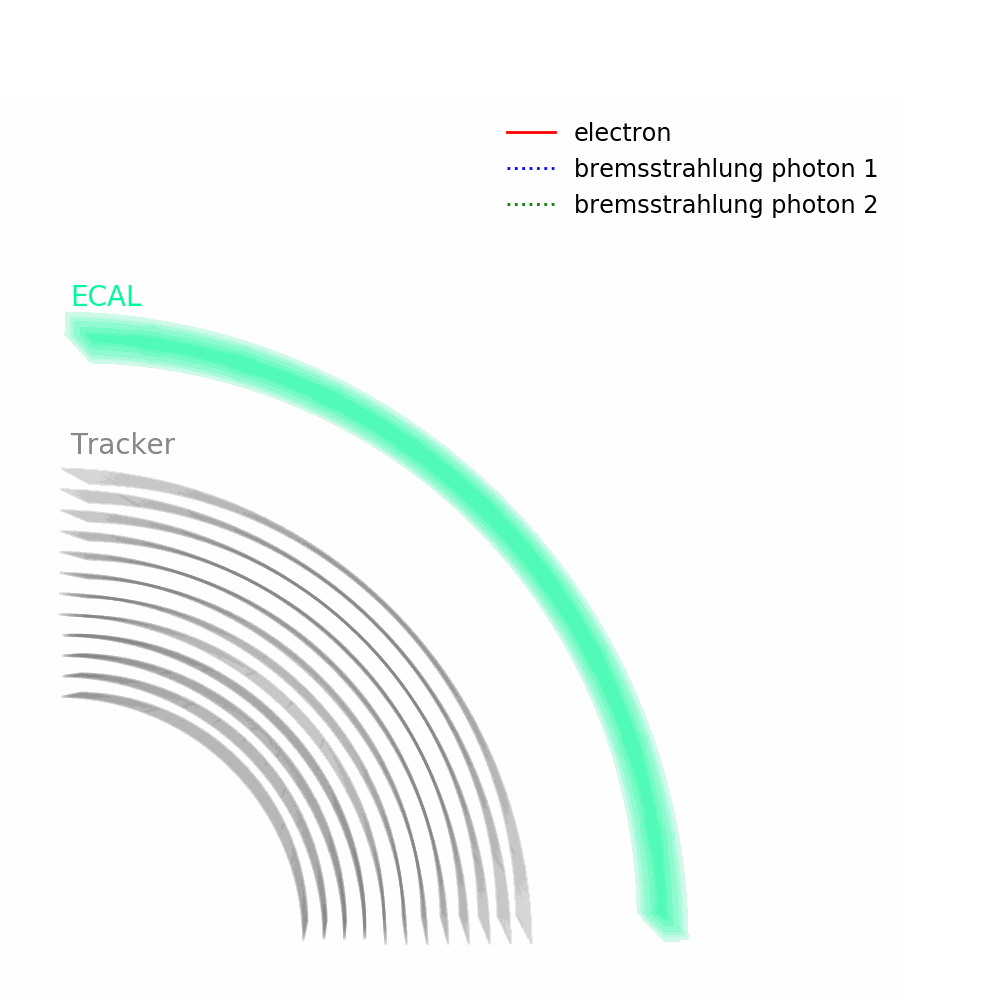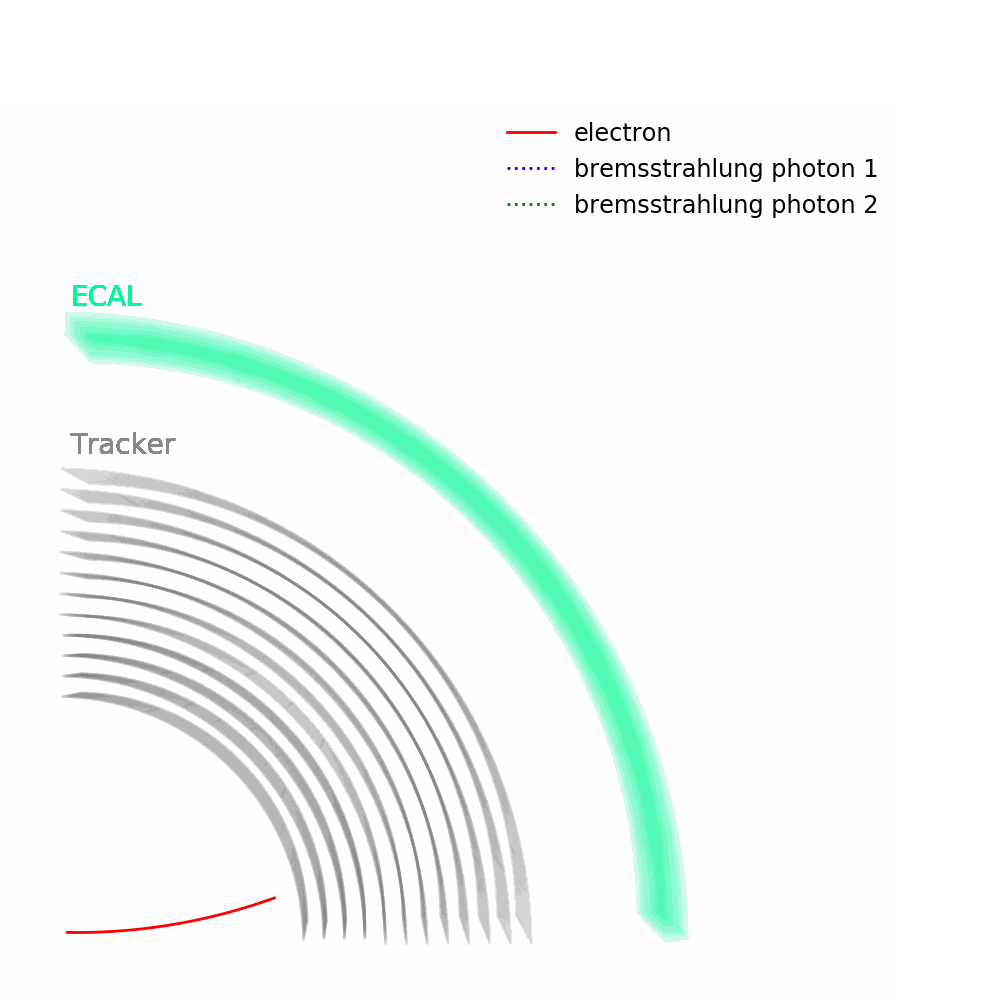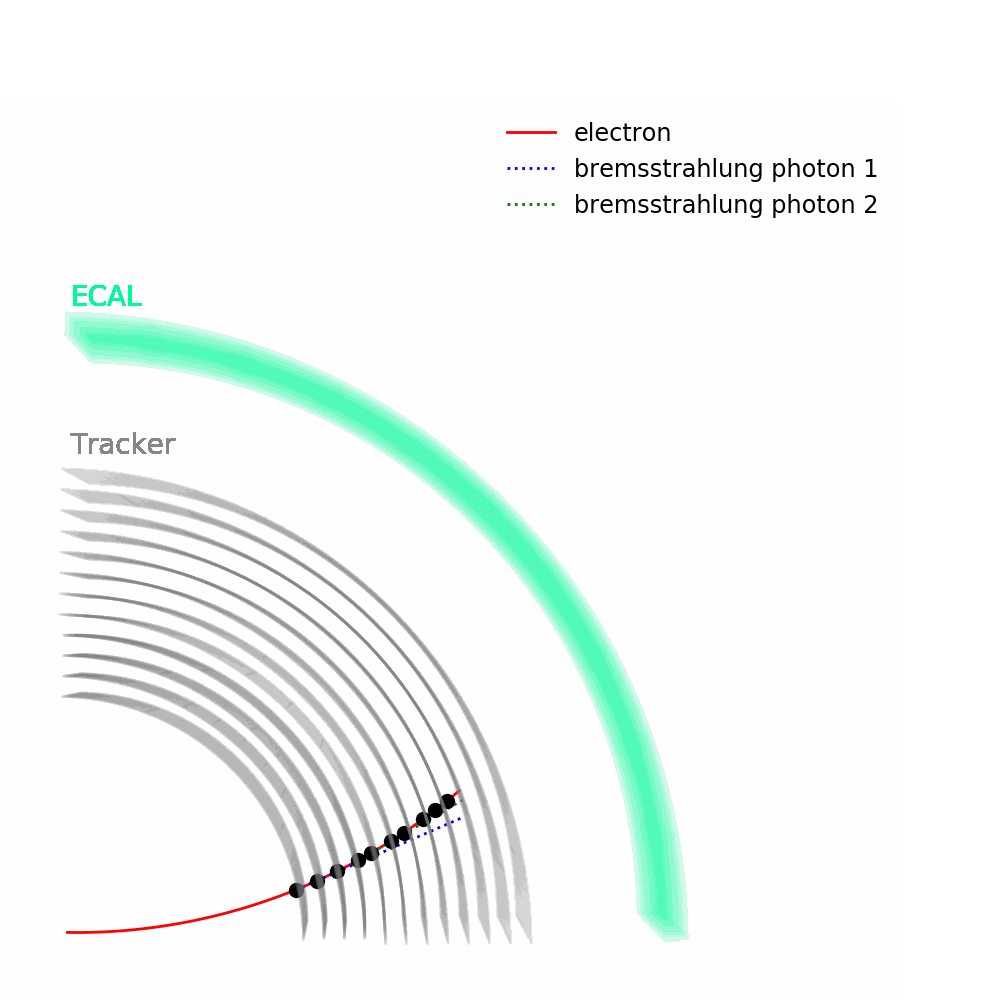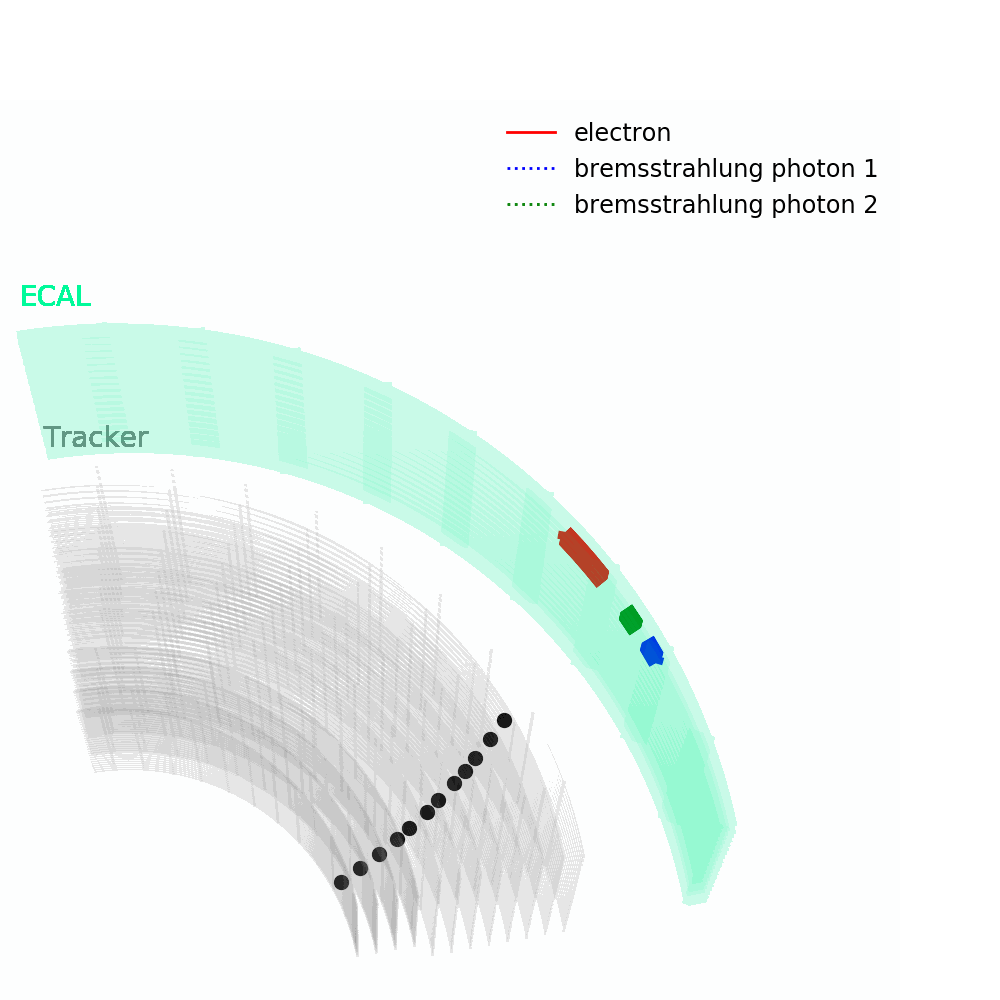
As depicted in the figure above, tracks – from the pixel and silicon tracker systems – as well as ECAL energy deposits are used to identify the passage of electrons in CMS. Being charged, electron trajectories curve inside the CMS magnetic field. Photons are similar objects but with no tracks. Sophisticated algorithms are run in the reconstruction to take into account subtleties related to the identification of an electromagnetic particle. An example is the convoluted showering of sub-photons and sub-electrons that can reach the ECAL due to bremsstrahlung and photon conversions.
We measure momentum and energy but also other properties of these objects that help analysts understand better their quality and origin.
Electron variables in NanoAOD
In the pre-exercises, you learned how to find NanoAOD datasets on the
Open Data Portal. One example is the SingleElectron dataset.
The “Dataset Semantics” section has a link to the variable
list webpage. Each “collection” of objects in the NanoAOD file is
linked by a common naming scheme (ex: Electron_*). The
individual variables are shown in a table that includes the branch name,
the data type, and a brief descriptive comment.
| Object property | Type | Description |
|---|---|---|
| Electron_charge | Int_t | electric charge |
| Electron_cleanmask | UChar_t | simple cleaning mask with priority to leptons |
| Electron_convVeto | Bool_t | pass conversion veto |
| Electron_cutBased | Int_t | cut-based ID Fall17 V2 (0:fail, 1:veto, 2:loose, 3:medium, 4:tight) |
| Electron_cutBased_HEEP | Bool_t | cut-based HEEP ID |
| Electron_dEscaleDown | Float_t | ecal energy scale shifted 1 sigma down (adding gain/stat/syst in quadrature) |
| Electron_dEscaleUp | Float_t | ecal energy scale shifted 1 sigma up(adding gain/stat/syst in quadrature) |
| Electron_dEsigmaDown | Float_t | ecal energy smearing value shifted 1 sigma up |
| Electron_dEsigmaUp | Float_t | ecal energy smearing value shifted 1 sigma up |
| Electron_deltaEtaSC | Float_t | delta eta (SC,ele) with sign |
| Electron_dr03EcalRecHitSumEt | Float_t | Non-PF Ecal isolation within a delta R cone of 0.3 with electron pt > 35 GeV |
| Electron_dr03HcalDepth1TowerSumEt | Float_t | Non-PF Hcal isolation within a delta R cone of 0.3 with electron pt > 35 GeV |
| Electron_dr03TkSumPt | Float_t | Non-PF track isolation within a delta R cone of 0.3 with electron pt > 35 GeV |
| Electron_dr03TkSumPtHEEP | Float_t | Non-PF track isolation within a delta R cone of 0.3 with electron pt > 35 GeV used in HEEP ID |
| Electron_dxy | Float_t | dxy (with sign) wrt first PV, in cm |
| Electron_dxyErr | Float_t | dxy uncertainty, in cm |
| Electron_dz | Float_t | dz (with sign) wrt first PV, in cm |
| Electron_dzErr | Float_t | dz uncertainty, in cm |
| Electron_eCorr | Float_t | ratio of the calibrated energy/miniaod energy |
| Electron_eInvMinusPInv | Float_t | 1/E_SC - 1/p_trk |
| Electron_energyErr | Float_t | energy error of the cluster-track combination |
| Electron_eta | Float_t | eta |
| Electron_hoe | Float_t | H over E |
| Electron_ip3d | Float_t | 3D impact parameter wrt first PV, in cm |
| Electron_isPFcand | Bool_t | electron is PF candidate |
| Electron_jetIdx | Int_t | (index to Jet) index of the associated jet (-1 if none) |
| Electron_jetNDauCharged | UChar_t | number of charged daughters of the closest jet |
| Electron_jetPtRelv2 | Float_t | Relative momentum of the lepton with respect to the closest jet after subtracting the lepton |
| Electron_jetRelIso | Float_t | Relative isolation in matched jet (1/ptRatio-1, pfRelIso04_all if no matched jet) |
| Electron_lostHits | UChar_t | number of missing inner hits |
| Electron_mass | Float_t | mass |
| Electron_miniPFRelIso_all | Float_t | mini PF relative isolation, total (with scaled rho*EA PU corrections) |
| Electron_miniPFRelIso_chg | Float_t | mini PF relative isolation, charged component |
| Electron_mvaFall17V2Iso | Float_t | MVA Iso ID V2 score |
| Electron_mvaFall17V2Iso_WP80 | Bool_t | MVA Iso ID V2 WP80 |
| Electron_mvaFall17V2Iso_WP90 | Bool_t | MVA Iso ID V2 WP90 |
| Electron_mvaFall17V2Iso_WPL | Bool_t | MVA Iso ID V2 loose WP |
| Electron_mvaFall17V2noIso | Float_t | MVA noIso ID V2 score |
| Electron_mvaFall17V2noIso_WP80 | Bool_t | MVA noIso ID V2 WP80 |
| Electron_mvaFall17V2noIso_WP90 | Bool_t | MVA noIso ID V2 WP90 |
| Electron_mvaFall17V2noIso_WPL | Bool_t | MVA noIso ID V2 loose WP |
| Electron_mvaTTH | Float_t | TTH MVA lepton ID score |
| Electron_pdgId | Int_t | PDG code assigned by the event reconstruction (not by MC truth) |
| Electron_pfRelIso03_all | Float_t | PF relative isolation dR=0.3, total (with rho*EA PU corrections) |
| Electron_pfRelIso03_chg | Float_t | PF relative isolation dR=0.3, charged component |
| Electron_phi | Float_t | phi |
| Electron_photonIdx | Int_t | (index to Photon) index of the associated photon (-1 if none) |
| Electron_pt | Float_t | p_{T} |
| Electron_r9 | Float_t | R9 of the supercluster, calculated with full 5x5 region |
| Electron_scEtOverPt | Float_t | (supercluster transverse energy)/pt-1 |
| Electron_seedGain | UChar_t | Gain of the seed crystal |
| Electron_sieie | Float_t | sigma_IetaIeta of the supercluster, calculated with full 5x5 region |
| Electron_sip3d | Float_t | 3D impact parameter significance wrt first PV, in cm |
| Electron_tightCharge | Int_t | Tight charge criteria (0:none, 1:isGsfScPixChargeConsistent, 2:isGsfCtfScPixChargeConsistent) |
| Electron_vidNestedWPBitmap | Int_t | VID compressed bitmap (MinPtCut,GsfEleSCEtaMultiRangeCut,GsfEleDEtaInSeedCut,GsfEleDPhiInCut,GsfEleFull5x5SigmaIEtaIEtaCut,GsfEleHadronicOverEMEnergyScaledCut,GsfEleEInverseMinusPInverseCut,GsfEleRelPFIsoScaledCut,GsfEleConversionVetoCut,GsfEleMissingHitsCut), 3 bits per cut |
| Electron_vidNestedWPBitmapHEEP | Int_t | VID compressed bitmap (MinPtCut,GsfEleSCEtaMultiRangeCut,GsfEleDEtaInSeedCut,GsfEleDPhiInCut,GsfEleFull5x5SigmaIEtaIEtaWithSatCut,GsfEleFull5x5E2x5OverE5x5WithSatCut,GsfEleHadronicOverEMLinearCut,GsfEleTrkPtIsoCut,GsfEleEmHadD1IsoRhoCut,GsfEleDxyCut,GsfEleMissingHitsCut,GsfEleEcalDrivenCut), 1 bits per cut |
| nElectron | UInt_t | slimmedElectrons after basic selection (pt > 5 ) |
Electron 4-vector and track information
All CMS physics objects contain basic 4-vector information: transverse momentum, pseudorapidity, azimuthal angle, and mass or energy:
| Object property | Type | Description |
|---|---|---|
| Electron_eta | Float_t | eta |
| Electron_mass | Float_t | mass |
| Electron_phi | Float_t | phi |
| Electron_pt | Float_t | p_{T} |
Most charged physics objects are also connected to tracks from the
CMS tracking detectors, and therefore the electric charge can be
identified from the track curvature. Electron charge can be computed
from 3 unique algorithms, so a tightCharge variable exists
to show when multiple of the charge determinations agree. Information
from tracks provides other kinematic quantities that are common to
multiple types of objects. Often, the most pertinent information about
an object to access from its associated track is its impact
parameter with respect to the primary interaction vertex. We
can access the impact parameters in the xy-plane (dxy or
d0) and along the beam axis (dz), as well as
their respective uncertainties. There is also a 3D impact parameter
significance that is very useful for identifying leptons that emerged
from a heavy flavor hadron decay.
| Object property | Type | Description |
|---|---|---|
| Electron_charge | Int_t | electric charge |
| Electron_dxy | Float_t | dxy (with sign) wrt first PV, in cm |
| Electron_dxyErr | Float_t | dxy uncertainty, in cm |
| Electron_dz | Float_t | dz (with sign) wrt first PV, in cm |
| Electron_dzErr | Float_t | dz uncertainty, in cm |
| Electron_sip3d | Float_t | 3D impact parameter significance wrt first PV, in cm |
| Electron_tightCharge | Int_t | Tight charge criteria (0:none, 1:isGsfScPixChargeConsistent, 2:isGsfCtfScPixChargeConsistent) |
Track-based info for photons
Note: in the case of Photons, since they are neutral objects, they do
not have a direct track link (though displaced track segments may appear
from electrons or positrons produced by the photon as it transits the
detector material). While the charge variable exists for
all objects, it is not used in photon analyses.
Detector information for identification
The most signicant difference between a list of certain particles from a Monte Carlo generator and a list of the corresponding physics objects from CMS is likely the inherent uncertainty in the reconstruction. Selection of “a muon” or “an electron” for analysis requires algorithms designed to separate “real” objects from “fakes”. These are called identification algorithms.
Other algorithms are designed to measure the amount of energy deposited near the object, to determine if it was likely produced near the primary interaction (typically little nearby energy), or from the decay of a longer-lived particle (typically a lot of nearby energy). These are called isolation algorithms. Many types of isolation algorithms exist to deal with unique physics cases!
Both types of algorithms function using working points that are described on a spectrum from “loose” to “tight”. Working points that are “looser” tend to have a high efficiency for accepting real objects, but perhaps a poor rejection rate for “fake” objects. Working points that are “tighter” tend to have lower efficiencies for accepting real objects, but much better rejection rates for “fake” objects. The choice of working point is highly analysis dependent! Some analyses value efficiency over background rejection, and some analyses are the opposite.
The standard identification and isolation algorithm results can be accessed from the physics object classes.
Multivariate Electron Identification (MVA)
In the Multi-variate Analysis (MVA) approach, one forms a single discriminator variable that is computed based on multiple parameters of the electron object and provides the best separation between the signal and backgrounds by means of multivariate analysis methods and statistical learning tools. One can then cut on discriminator value or use the distribution of the values for a shape based statistical analysis.
There are two basic types of MVAs that are were trained by CMS for 2016 electrons:
- MVA with isolation: the MVA includes standard particle-flow isolation as one of the variables used for training. This MVA is well suited for analyses considering typical prompt electrons that are likely to be isolated from jets or other objects.
- MVA without isolation: no isolation variables are included for training. This MVA is better suited for analyses in which the electrons might be poorly isolated from jets or other objects.
Both MVAs were assigned working points with 80% efficiency (WP80), 90% efficiency (WP90), and a very high efficiency (“loose”)
| Object property | Type | Description |
|---|---|---|
| Electron_mvaFall17V2Iso | Float_t | MVA Iso ID V2 score |
| Electron_mvaFall17V2Iso_WP80 | Bool_t | MVA Iso ID V2 WP80 |
| Electron_mvaFall17V2Iso_WP90 | Bool_t | MVA Iso ID V2 WP90 |
| Electron_mvaFall17V2Iso_WPL | Bool_t | MVA Iso ID V2 loose WP |
| Electron_mvaFall17V2noIso | Float_t | MVA noIso ID V2 score |
| Electron_mvaFall17V2noIso_WP80 | Bool_t | MVA noIso ID V2 WP80 |
| Electron_mvaFall17V2noIso_WP90 | Bool_t | MVA noIso ID V2 WP90 |
| Electron_mvaFall17V2noIso_WPL | Bool_t | MVA noIso ID V2 loose WP |
Cut Based Electron ID
Electron identification can also be evaluated without MVAs, using a set of “cut-based” identification criteria:
| Object property | Type | Description |
|---|---|---|
| Electron_cutBased | Int_t | cut-based ID Fall17 V2 (0:fail, 1:veto, 2:loose, 3:medium, 4:tight) |
| Electron_cutBased_HEEP | Bool_t | cut-based HEEP ID |
Four standard working points are provided * Veto (average efficiency ~95%). Use this working point for third lepton veto or counting. * Loose (average efficiency ~90%). Use this working point when backgrounds are rather low. * Medium (average efficiency ~80%). This is a good starting point for generic measurements involving W or Z bosons. * Tight (average efficiency ~70%). Use this working point for measurements where backgrounds are a serious problem.
All of the cut-based working points include particle-flow isolation
requirements. The HEEP identifier is specifically intended
to improve efficiency for high-energy electrons with more than 100-200
GeV of transverse momentum.
Electron isolation
Isolation is computed in similar ways for all physics objects: search for particles in a cone around the object of interest and sum up their energies, subtracting off the energy deposited by pileup particles. This sum divided by the object of interest’s transverse momentum is called relative isolation and is the most common way to determine whether an object was produced “promptly” in or following the proton-proton collision (ex: electrons from a Z boson decay, or photons from a Higgs boson decay). Relative isolation values will tend to be large for particles that emerged from weak decays of hadrons within jets, or other similar “nonprompt” processes.
While many of the electron identification algorithms include isolation, the isolation values are also available:
| Object property | Type | Description |
|---|---|---|
| Electron_dr03EcalRecHitSumEt | Float_t | Non-PF Ecal isolation within a delta R cone of 0.3 with electron pt > 35 GeV |
| Electron_dr03HcalDepth1TowerSumEt | Float_t | Non-PF Hcal isolation within a delta R cone of 0.3 with electron pt > 35 GeV |
| Electron_dr03TkSumPt | Float_t | Non-PF track isolation within a delta R cone of 0.3 with electron pt > 35 GeV |
| Electron_dr03TkSumPtHEEP | Float_t | Non-PF track isolation within a delta R cone of 0.3 with electron pt > 35 GeV used in HEEP ID |
| Electron_pfRelIso03_all | Float_t | PF relative isolation dR=0.3, total (with rho*EA PU corrections) |
| Electron_pfRelIso03_chg | Float_t | PF relative isolation dR=0.3, charged component |
Electron cross-reference indices
Electrons can be associated with both jets and photons based on the particle-flow algorithm. Since the jet and photon collections have independent array structures, the indices of the matched jet or photon is provided in the electron collection:
| Object property | Type | Description |
|---|---|---|
| Electron_jetIdx | Int_t | (index to Jet) index of the associated jet (-1 if none) |
| Electron_photonIdx | Int_t | (index to Photon) index of the associated photon (-1 if none) |
Photons
Since photons are also primarily reconstructed as electromagnetic calorimeter showers, the vast majority of their reconstruction methods are common with electrons. Photons also have 4-vector, identification, and isolation information available in NanoAOD
| Object property | Type | Description |
|---|---|---|
| Photon_charge | Int_t | electric charge |
| Photon_cleanmask | UChar_t | simple cleaning mask with priority to leptons |
| Photon_cutBased | Int_t | cut-based ID bitmap, Fall17V2, (0:fail, 1:loose, 2:medium, 3:tight) |
| Photon_cutBased_Fall17V1Bitmap | Int_t | cut-based ID bitmap, Fall17V1, 2^(0:loose, 1:medium, 2:tight). |
| Photon_dEscaleDown | Float_t | ecal energy scale shifted 1 sigma down (adding gain/stat/syst in quadrature) |
| Photon_dEscaleUp | Float_t | ecal energy scale shifted 1 sigma up (adding gain/stat/syst in quadrature) |
| Photon_dEsigmaDown | Float_t | ecal energy smearing value shifted 1 sigma up |
| Photon_dEsigmaUp | Float_t | ecal energy smearing value shifted 1 sigma up |
| Photon_eCorr | Float_t | ratio of the calibrated energy/miniaod energy |
| Photon_electronIdx | Int_t (index to Electron) | index of the associated electron (-1 if none) |
| Photon_electronVeto | Bool_t | pass electron veto |
| Photon_energyErr | Float_t | energy error of the cluster from regression |
| Photon_eta | Float_t | eta |
| Photon_hoe | Float_t | H over E |
| Photon_isScEtaEB | Bool_t | is supercluster eta within barrel acceptance |
| Photon_isScEtaEE | Bool_t | is supercluster eta within endcap acceptance |
| Photon_jetIdx | Int_t | (index to Jet) index of the associated jet (-1 if none) |
| Photon_mass | Float_t | mass |
| Photon_mvaID | Float_t | MVA ID score, Fall17V2 |
| Photon_mvaID_Fall17V1p1 | Float_t | MVA ID score, Fall17V1p1 |
| Photon_mvaID_WP80 | Bool_t | MVA ID WP80, Fall17V2 |
| Photon_mvaID_WP90 | Bool_t | MVA ID WP90, Fall17V2 |
| Photon_pdgId | Int_t | PDG code assigned by the event reconstruction (not by MC truth) |
| Photon_pfRelIso03_all | Float_t | PF relative isolation dR=0.3, total (with rho*EA PU corrections) |
| Photon_pfRelIso03_chg | Float_t | PF relative isolation dR=0.3, charged component (with rho*EA PU corrections) |
| Photon_phi | Float_t | phi |
| Photon_pixelSeed | Bool_t | has pixel seed |
| Photon_pt | Float_t | p_{T} |
| Photon_r9 | Float_t | R9 of the supercluster, calculated with full 5x5 region |
| Photon_seedGain | UChar_t | Gain of the seed crystal |
| Photon_sieie | Float_t | sigma_IetaIeta of the supercluster, calculated with full 5x5 region |
| Photon_vidNestedWPBitmap | Int_t | Fall17V2 VID compressed bitmap (MinPtCut,PhoSCEtaMultiRangeCut,PhoSingleTowerHadOverEmCut,PhoFull5x5SigmaIEtaIEtaCut,PhoGenericRhoPtScaledCut,PhoGenericRhoPtScaledCut,PhoGenericRhoPtScaledCut), 2 bits per cut |
| nPhoton | UInt_t | slimmedPhotons after basic selection (pt > 5 ) |
Key Points
- Quantities such as impact parameters and charge have common member functions.
- Physics objects in CMS are reconstructed from detector signals and are never 100% certain!
- Identification and isolation algorithms are important for reducing fake objects.
Content from Muons & Taus
Last updated on 2024-07-09 | Edit this page
Overview
Questions
- How are muons reconstructed in CMS?
- How are muons treated in CMS OpenData?
Objectives
- Understand how muons are reconstructed in CMS
- Learn variables for muon track-based quantities
- Learn variables for identification and isolation of muons
Overview of muon reconstruction
Muons are the M in CMS (Compact Muon Solenoid). This is in part because they are reconstructed basically using all the CMS sub-detectors. As it nicely summarized here:
[A muon] is measured by fitting a curve to the hits registered in the four muon stations, which are located outside of the magnet coil, interleaved with iron “return yoke” plates. The particle path is measured by tracking its position through the multiple active layers of each station; for improved precision, this information is combined with the CMS silicon tracker measurements. Measuring the trajectory provides a measurement of particle momentum. Indeed, the strong magnetic field generated by the CMS solenoid bends the particle’s trajectory, with a bending radius that depends on its momentum: the more straight the track, the higher the momentum.
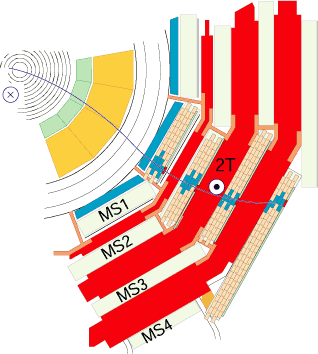
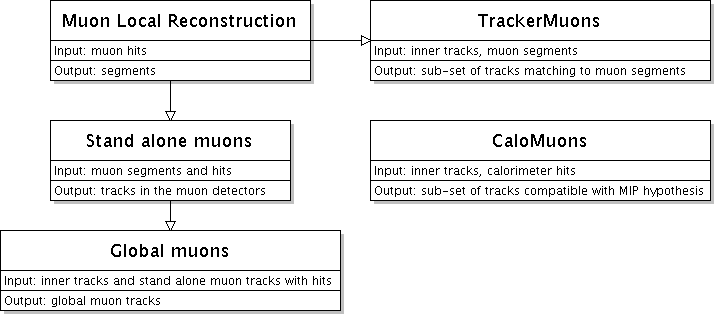
Depending essentially on the kind of sub-detectors were used to reconstruct muons, they are usually classified accroding to the summary image below.
Muons have many features in common with electrons, but their own unique identification algorithms. We will use the same NanoAOD file as in the previous episode to look at the Muon NanoAOD branches.
| Object property | Type | Description |
|---|---|---|
| Muon_charge | Int_t | electric charge |
| Muon_cleanmask | UChar_t | simple cleaning mask with priority to leptons |
| Muon_dxy | Float_t | dxy (with sign) wrt first PV, in cm |
| Muon_dxyErr | Float_t | dxy uncertainty, in cm |
| Muon_dxybs | Float_t | dxy (with sign) wrt the beam spot, in cm |
| Muon_dz | Float_t | dz (with sign) wrt first PV, in cm |
| Muon_dzErr | Float_t | dz uncertainty, in cm |
| Muon_eta | Float_t | eta |
| Muon_fsrPhotonIdx | Int_t | (index to Fsrphoton) Index of the associated FSR photon |
| Muon_highPtId | UChar_t | high-pT cut-based ID (1 = tracker high pT, 2 = global high pT, which includes tracker high pT) |
| Muon_highPurity | Bool_t | inner track is high purity |
| Muon_inTimeMuon | Bool_t | inTimeMuon ID |
| Muon_ip3d | Float_t | 3D impact parameter wrt first PV, in cm |
| Muon_isGlobal | Bool_t | muon is global muon |
| Muon_isPFcand | Bool_t | muon is PF candidate |
| Muon_isStandalone | Bool_t | muon is a standalone muon |
| Muon_isTracker | Bool_t | muon is tracker muon |
| Muon_jetIdx | Int_t | (index to Jet) index of the associated jet (-1 if none) |
| Muon_jetNDauCharged | UChar_t | number of charged daughters of the closest jet |
| Muon_jetPtRelv2 | Float_t | Relative momentum of the lepton with respect to the closest jet after subtracting the lepton |
| Muon_jetRelIso | Float_t | Relative isolation in matched jet (1/ptRatio-1, pfRelIso04_all if no matched jet) |
| Muon_looseId | Bool_t | muon is loose muon |
| Muon_mass | Float_t | mass |
| Muon_mediumId | Bool_t | cut-based ID, medium WP |
| Muon_mediumPromptId | Bool_t | cut-based ID, medium prompt WP |
| Muon_miniIsoId | UChar_t | MiniIso ID from miniAOD selector (1=MiniIsoLoose, 2=MiniIsoMedium, 3=MiniIsoTight, 4=MiniIsoVeryTight) |
| Muon_miniPFRelIso_all | Float_t | mini PF relative isolation, total (with scaled rho*EA PU corrections) |
| Muon_miniPFRelIso_chg | Float_t | mini PF relative isolation, charged component |
| Muon_multiIsoId | UChar_t | MultiIsoId from miniAOD selector (1=MultiIsoLoose, 2=MultiIsoMedium) |
| Muon_mvaId | UChar_t | Mva ID from miniAOD selector (1=MvaLoose, 2=MvaMedium, 3=MvaTight, 4=MvaVTight, 5=MvaVVTight) |
| Muon_mvaLowPt | Float_t | Low pt muon ID score |
| Muon_mvaLowPtId | UChar_t | Low Pt Mva ID from miniAOD selector (1=LowPtMvaLoose, 2=LowPtMvaMedium) |
| Muon_mvaTTH | Float_t | TTH MVA lepton ID score |
| Muon_nStations | Int_t | number of matched stations with default arbitration (segment & track) |
| Muon_nTrackerLayers | Int_t | number of layers in the tracker |
| Muon_pdgId | Int_t | PDG code assigned by the event reconstruction (not by MC truth) |
| Muon_pfIsoId | UChar_t | PFIso ID from miniAOD selector (1=PFIsoVeryLoose, 2=PFIsoLoose, 3=PFIsoMedium, 4=PFIsoTight, 5=PFIsoVeryTight, 6=PFIsoVeryVeryTight) |
| Muon_pfRelIso03_all | Float_t | PF relative isolation dR=0.3, total (deltaBeta corrections) |
| Muon_pfRelIso03_chg | Float_t | PF relative isolation dR=0.3, charged component |
| Muon_pfRelIso04_all | Float_t | PF relative isolation dR=0.4, total (deltaBeta corrections) |
| Muon_phi | Float_t | phi |
| Muon_pt | Float_t | pt |
| Muon_ptErr | Float_t | ptError of the muon track |
| Muon_puppiIsoId | UChar_t | PuppiIsoId from miniAOD selector (1=Loose, 2=Medium, 3=Tight) |
| Muon_segmentComp | Float_t | muon segment compatibility |
| Muon_sip3d | Float_t | 3D impact parameter significance wrt first PV |
| Muon_softId | Bool_t | soft cut-based ID |
| Muon_softMva | Float_t | soft MVA ID score |
| Muon_softMvaId | Bool_t | soft MVA ID |
| Muon_tightCharge | Int_t | Tight charge criterion using pterr/pt of muonBestTrack (0:fail, 2:pass) |
| Muon_tightId | Bool_t | cut-based ID, tight WP |
| Muon_tkIsoId | UChar_t | TkIso ID (1=TkIsoLoose, 2=TkIsoTight) |
| Muon_tkRelIso | Float_t | Tracker-based relative isolation dR=0.3 for highPt, trkIso/tunePpt |
| Muon_triggerIdLoose | Bool_t | TriggerIdLoose ID |
| Muon_tunepRelPt | Float_t | TuneP relative pt, tunePpt/pt |
| nMuon | UInt_t | slimmedMuons after basic selection (pt > 15 |
Muon 4-vector and track-related variables
These branches for muons are very similar to those we saw earlier for electrons:
-
pt,eta,phi, andmassform the 4-vector -
chargeandtightChargegive electric charge information -
dxy,dz,ip3d, and their uncertainties or significances give impact parameter information
| Object property | Type | Description |
|---|---|---|
| Muon_charge | Int_t | electric charge |
| Muon_dxy | Float_t | dxy (with sign) wrt first PV, in cm |
| Muon_dxyErr | Float_t | dxy uncertainty, in cm |
| Muon_dxybs | Float_t | dxy (with sign) wrt the beam spot, in cm |
| Muon_dz | Float_t | dz (with sign) wrt first PV, in cm |
| Muon_dzErr | Float_t | dz uncertainty, in cm |
| Muon_eta | Float_t | eta |
| Muon_ip3d | Float_t | 3D impact parameter wrt first PV, in cm |
| Muon_mass | Float_t | mass |
| Muon_phi | Float_t | phi |
| Muon_pt | Float_t | pt |
| Muon_sip3d | Float_t | 3D impact parameter significance wrt first PV |
| Muon_tightCharge | Int_t | Tight charge criterion using pterr/pt of muonBestTrack (0:fail, 2:pass) |
Muon identification and isolation
The CMS Muon object group has created member functions for the
identification algorithms that store pass/fail decisions about the
quality of each muon. A set of cut-based identification working points
are available: looseId, mediumId,
mediumPromptId, softId, highPtId.
Another set of identification algorithms are based on MVA discriminants:
mvaId, mvaLowPtId, mvaTTH,
softMvaId.
| Object property | Type | Description |
|---|---|---|
| Muon_highPtId | UChar_t | high-pT cut-based ID (1 = tracker high pT, 2 = global high pT, which includes tracker high pT) |
| Muon_looseId | Bool_t | muon is loose muon |
| Muon_mediumId | Bool_t | cut-based ID, medium WP |
| Muon_mediumPromptId | Bool_t | cut-based ID, medium prompt WP |
| Muon_mvaId | UChar_t | Mva ID from miniAOD selector (1=MvaLoose, 2=MvaMedium, 3=MvaTight, 4=MvaVTight, 5=MvaVVTight) |
| Muon_mvaLowPtId | UChar_t | Low Pt Mva ID from miniAOD selector (1=LowPtMvaLoose, 2=LowPtMvaMedium) |
| Muon_mvaTTH | Float_t | TTH MVA lepton ID score |
| Muon_softId | Bool_t | soft cut-based ID |
| Muon_softMvaId | Bool_t | soft MVA ID |
| Muon_tightId | Bool_t | cut-based ID, tight WP |
Hard processes produce large angles between the final state partons. The final object of interest will be separated from the other objects in the event or be isolated. For instance, an isolated muon might be produced in the decay of a W boson. In contrast, a non-isolated muon can come from a weak decay inside a jet.
Muon isolation is calculated from a combination of factors: energy from charged hadrons, energy from neutral hadrons, and energy from photons, all in a cone of radius \(R = \sqrt{\eta^2 + \phi^2} < 0.3\) or \(<0.4\) around the muon. Many algorithms also feature a correction factor that subtracts average energy expected from pileup contributions to this con. The sum of the \(p_{T}\) of the charged hadrons associated to vertices other than the primary vertex, is used to correct for pileup contamination in the total flux of neutrals found in the muon isolation cone. A factor of \(\beta = 0.5\) is used to scale this contribution as:
\(I_{\mu} = \frac{1}{p_{T}} \sum_{R<0.4} \left( p_{T}^{\mathrm{charged\,hadrons}} + \max(p_{T}^{\mathrm{photons}} + p_{T}^{\mathrm{neutral\,hadrons}} - \beta p_{T}^{\mathrm{charged\,pileup}} , 0) \right)\)
Many forms of muon isolation are stored in NanoAOD, as shown in the
table. The primary particle-flow isolation variable is
Muon_pfIsoId. Another type of isolation in common us is
“mini”-isolation, Muon_miniIsoId, which adapts the size of
the cone to improve efficiency for leptons that might exist near jets
because they were decay products of a high-momentum particle, such as a
top quark.
| Object property | Type | Description |
|---|---|---|
| Muon_jetRelIso | Float_t | Relative isolation in matched jet (1/ptRatio-1, pfRelIso04_all if no matched jet) |
| Muon_miniIsoId | UChar_t | MiniIso ID from miniAOD selector (1=MiniIsoLoose, 2=MiniIsoMedium, 3=MiniIsoTight, 4=MiniIsoVeryTight) |
| Muon_miniPFRelIso_all | Float_t | mini PF relative isolation, total (with scaled rho*EA PU corrections) |
| Muon_miniPFRelIso_chg | Float_t | mini PF relative isolation, charged component |
| Muon_multiIsoId | UChar_t | MultiIsoId from miniAOD selector (1=MultiIsoLoose, 2=MultiIsoMedium) |
| Muon_pfIsoId | UChar_t | PFIso ID from miniAOD selector (1=PFIsoVeryLoose, 2=PFIsoLoose, 3=PFIsoMedium, 4=PFIsoTight, 5=PFIsoVeryTight, 6=PFIsoVeryVeryTight) |
| Muon_pfRelIso03_all | Float_t | PF relative isolation dR=0.3, total (deltaBeta corrections) |
| Muon_pfRelIso03_chg | Float_t | PF relative isolation dR=0.3, charged component |
| Muon_pfRelIso04_all | Float_t | PF relative isolation dR=0.4, total (deltaBeta corrections) |
| Muon_puppiIsoId | UChar_t | PuppiIsoId from miniAOD selector (1=Loose, 2=Medium, 3=Tight) |
| Muon_tkIsoId | UChar_t | TkIso ID (1=TkIsoLoose, 2=TkIsoTight) |
| Muon_tkRelIso | Float_t | Tracker-based relative isolation dR=0.3 for highPt, trkIso/tunePpt |
Muon cross-reference indices
Like electrons, muons can be cross-referenced to other arrays in the NanoAOD file:
| Object property | Type | Description |
|---|---|---|
| Muon_fsrPhotonIdx | Int_t | (index to Fsrphoton) Index of the associated FSR photon |
| Muon_jetIdx | Int_t | (index to Jet) index of the associated jet (-1 if none) |
Tau leptons
The CMS Tau object group relies almost entirely on pre-computed algorithms to determine the quality of the tau reconstruction and the decay type. Since this object is not stable and has several decay modes, different combinations of identification and isolation algorithms are used across different analyses. The Run 1 Tau ID page and Nutshell Recipe provide a large table of algorithms that remains a valuable reference.
Taus that decay to leptons are typically identified as electrons or muons in CMS. But taus that decay to hadrons can be identified in the calorimeters based on the characteristic size and shape of their clusters.
| Object property | Type | Description |
|---|---|---|
| Tau_charge | Int_t | electric charge |
| Tau_chargedIso | Float_t | charged isolation |
| Tau_cleanmask | UChar_t | simple cleaning mask with priority to leptons |
| Tau_decayMode | Int_t | decayMode() |
| Tau_dxy | Float_t | d_{xy} of lead track with respect to PV, in cm (with sign) |
| Tau_dz | Float_t | d_{z} of lead track with respect to PV, in cm (with sign) |
| Tau_eta | Float_t | eta |
| Tau_idAntiEleDeadECal | Bool_t | Anti-electron dead-ECal discriminator |
| Tau_idAntiMu | UChar_t | Anti-muon discriminator V3: : bitmask 1 = Loose, 2 = Tight |
| Tau_idDecayModeOldDMs | Bool_t | tauID(‘decayModeFinding’) |
| Tau_idDeepTau2017v2p1VSe | UChar_t | byDeepTau2017v2p1VSe ID working points (deepTau2017v2p1): bitmask 1 = VVVLoose, 2 = VVLoose, 4 = VLoose, 8 = Loose, 16 = Medium, 32 = Tight, 64 = VTight, 128 = VVTight |
| Tau_idDeepTau2017v2p1VSjet | UChar_t | byDeepTau2017v2p1VSjet ID working points (deepTau2017v2p1): bitmask 1 = VVVLoose, 2 = VVLoose, 4 = VLoose, 8 = Loose, 16 = Medium, 32 = Tight, 64 = VTight, 128 = VVTight |
| Tau_idDeepTau2017v2p1VSmu | UChar_t | byDeepTau2017v2p1VSmu ID working points (deepTau2017v2p1): bitmask 1 = VLoose, 2 = Loose, 4 = Medium, 8 = Tight |
| Tau_jetIdx | Int_t | (index to Jet) index of the associated jet (-1 if none) |
| Tau_leadTkDeltaEta | Float_t | eta of the leading track, minus tau eta |
| Tau_leadTkDeltaPhi | Float_t | phi of the leading track, minus tau phi |
| Tau_leadTkPtOverTauPt | Float_t | pt of the leading track divided by tau pt |
| Tau_mass | Float_t | mass |
| Tau_neutralIso | Float_t | neutral (photon) isolation |
| Tau_phi | Float_t | phi |
| Tau_photonsOutsideSignalCone | Float_t | sum of photons outside signal cone |
| Tau_pt | Float_t | pt |
| Tau_puCorr | Float_t | pileup correction |
| Tau_rawDeepTau2017v2p1VSe | Float_t | byDeepTau2017v2p1VSe raw output discriminator (deepTau2017v2p1) |
| Tau_rawDeepTau2017v2p1VSjet | Float_t | byDeepTau2017v2p1VSjet raw output discriminator (deepTau2017v2p1) |
| Tau_rawDeepTau2017v2p1VSmu | Float_t | byDeepTau2017v2p1VSmu raw output discriminator (deepTau2017v2p1) |
| Tau_rawIso | Float_t | combined isolation (deltaBeta corrections) |
| Tau_rawIsodR03 | Float_t | combined isolation (deltaBeta corrections, dR=0.3) |
| nTau | UInt_t | slimmedTaus after basic selection (pt > 18 && tauID(‘decayModeFindingNewDMs’) && (tauID(‘byLooseCombinedIsolationDeltaBetaCorr3Hits’) |
Tau identification variables
The following variables in the tau collection represent the identification and isolation variables.
| Object property | Type | Description |
|---|---|---|
| Tau_decayMode | Int_t | decayMode() |
| Tau_idAntiEleDeadECal | Bool_t | Anti-electron dead-ECal discriminator |
| Tau_idAntiMu | UChar_t | Anti-muon discriminator V3: : bitmask 1 = Loose, 2 = Tight |
| Tau_idDecayModeOldDMs | Bool_t | tauID(‘decayModeFinding’) |
| Tau_idDeepTau2017v2p1VSe | UChar_t | byDeepTau2017v2p1VSe ID working points (deepTau2017v2p1): bitmask 1 = VVVLoose, 2 = VVLoose, 4 = VLoose, 8 = Loose, 16 = Medium, 32 = Tight, 64 = VTight, 128 = VVTight |
| Tau_idDeepTau2017v2p1VSjet | UChar_t | byDeepTau2017v2p1VSjet ID working points (deepTau2017v2p1): bitmask 1 = VVVLoose, 2 = VVLoose, 4 = VLoose, 8 = Loose, 16 = Medium, 32 = Tight, 64 = VTight, 128 = VVTight |
| Tau_idDeepTau2017v2p1VSmu | UChar_t | byDeepTau2017v2p1VSmu ID working points (deepTau2017v2p1): bitmask 1 = VLoose, 2 = Loose, 4 = Medium, 8 = Tight |
| Tau_rawIso | Float_t | combined isolation (deltaBeta corrections) |
| Tau_rawIsodR03 | Float_t | combined isolation (deltaBeta corrections, dR=0.3) |
Other tau information
Information about the tau lepton 4-vectors, cross-reference indices, impact parameters, etc, are analogous to the variables for electrons and muons.
Key Points
- Track access may differ, but track-related member functions are common across objects.
- Physics objects in CMS are reconstructed from detector signals and are never 100% certain!
- Muons typically use pre-configured identification and isolation variables”
Content from Jets and MET
Last updated on 2024-07-09 | Edit this page
Overview
Questions
- How are jets and missing transverse energy treated in CMS Open Data?
Objectives
- Identify jet and MET code collections in AOD files
- Understand typical features of jet/MET objects
After tracks and energy deposits in the CMS tracking detectors (inner, muon) and calorimeters (electromagnetic, hadronic) are reconstructed as particle flow candidates, an event can be interpreted in various ways. Two common elements of event interpretation are clustering jets and calculating missing transverse momentum.
Jets
Jets are spatially-grouped collections of long-lived particles that are produced when a quark or gluon hadronizes. The kinetmatic properties of jets resemble that of the initial partons that produced them. In the CMS language, jets are made up of many particles, with the following predictable energy composition:
- ~65% charged hadrons
- ~25% photons (from neutral pions)
- ~10% neutral hadrons
Jets are very messy! Hadronization and the subsequent decays of unstable hadrons can produce 100s of particles near each other in the CMS detector. Hence these particles are rarely analyzed individually. How can we determine which particle candidates should be included in each jet?
Clustering
Jets can be clustered using a variety of different inputs from the CMS detector. “CaloJets” use only calorimeter energy deposits. “GenJets” use generated particles from a simulation. But by far the most common are “PFJets”, from particle flow candidates.
The result of the CMS Particle Flow algorithm is a list of particle candidates that account for all inner-tracker and muon tracks and all above-threshold energy deposits in the calorimeters. These particles are formed into jets using a “clustering algorithm”. The most common algorithm used by CMS is the “anti-kt” algorithm, which is abbreviated “AK”. It iterates over particle pairs and finds the two (i and j) that are the closest in some distance measure and determines whether to combine them:
\(d_{ij} = \min(p^{-2}_{T,i},p^{-2}_{T,j}) \Delta R^2_{ij}/R^2\)
Particle pairs are combined as long as \(d_{ij} < p^{-2}_{T,i}\). The momentum power (-2) used by the anti-kt algorithm means that higher-momentum particles are clustered first. This leads to jets with a round shape that tend to be centered on the hardest particle. In CMS software this clustering is implemented using the FastJet package.
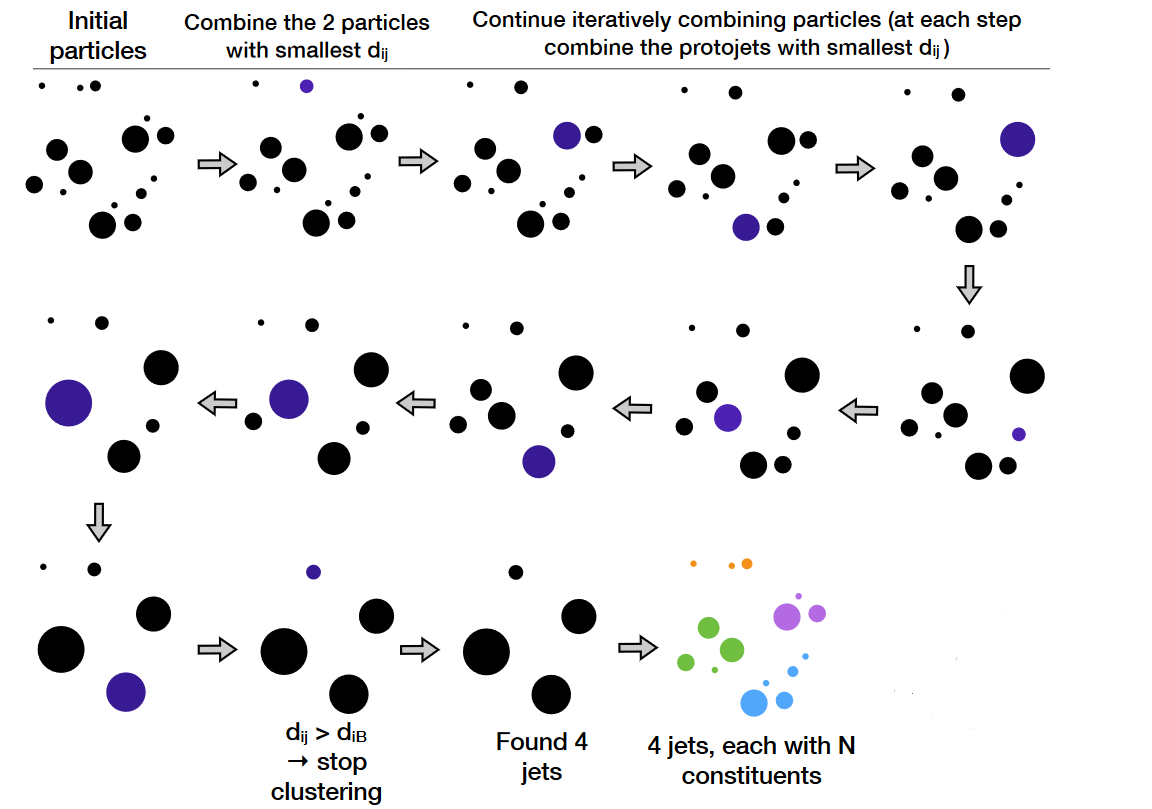
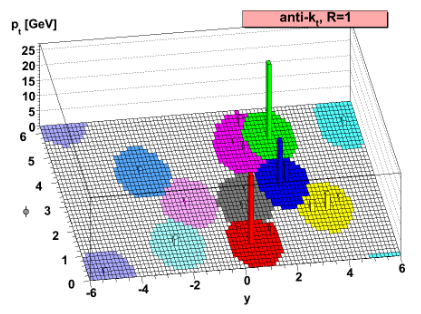
Pileup
Inevitably, the list of particle flow candidates contains particles that did not originate from the primary interaction point. CMS experiences multiple simultaneous collisions, called “pileup”, during each “bunch crossing” of the LHC, so particles from multiple collisions coexist in the detector. There are various methods to remove their contributions from jets:
- Charged hadron subtraction CHS: all charged hadron candidates are associated with a track. If the track is not associated with the primary vertex, that charged hadron can be removed from the list. CHS is limited to the region of the detector covered by the inner tracker. The pileup contribution to neutral hadrons has to be removed mathematically – more in episode 3!
- PileUp Per Particle Identification (PUPPI, available in Run 2): CHS is applied, and then all remaining particles are weighted based on their likelihood of arising from pileup. This method is more stable and performant in high pileup scenarios such as the upcoming HL-LHC era.
Small-radius jets in NanoAOD
The most basic setting for anti-kt particle-flow jets in CMS is a radius parameter of 0.4. These jets are often called “AK4 jets” or “small-radius jets”. Their information is stored in the “Jet_*” collection in NanoAOD:
| Object property | Type | Description |
|---|---|---|
| Jet_area | Float_t | jet catchment area, for JECs |
| Jet_bRegCorr | Float_t | pt correction for b-jet energy regression |
| Jet_bRegRes | Float_t | res on pt corrected with b-jet regression |
| Jet_btagCSVV2 | Float_t | pfCombinedInclusiveSecondaryVertexV2 b-tag discriminator (aka CSVV2) |
| Jet_btagDeepB | Float_t | DeepCSV b+bb tag discriminator |
| Jet_btagDeepCvB | Float_t | DeepCSV c vs b+bb discriminator |
| Jet_btagDeepCvL | Float_t | DeepCSV c vs udsg discriminator |
| Jet_btagDeepFlavB | Float_t | DeepJet b+bb+lepb tag discriminator |
| Jet_btagDeepFlavCvB | Float_t | DeepJet c vs b+bb+lepb discriminator |
| Jet_btagDeepFlavCvL | Float_t | DeepJet c vs uds+g discriminator |
| Jet_btagDeepFlavQG | Float_t | DeepJet g vs uds discriminator |
| Jet_cRegCorr | Float_t | pt correction for c-jet energy regression |
| Jet_cRegRes | Float_t | res on pt corrected with c-jet regression |
| Jet_chEmEF | Float_t | charged Electromagnetic Energy Fraction |
| Jet_chFPV0EF | Float_t | charged fromPV==0 Energy Fraction (energy excluded from CHS jets). Previously called betastar. |
| Jet_chHEF | Float_t | charged Hadron Energy Fraction |
| Jet_cleanmask | UChar_t | simple cleaning mask with priority to leptons |
| Jet_electronIdx1 | Int_t | (index to Electron) index of first matching electron |
| Jet_electronIdx2 | Int_t | (index to Electron) index of second matching electron |
| Jet_eta | Float_t | eta |
| Jet_hfadjacentEtaStripsSize | Int_t | eta size of the strips next to the central tower strip in HF (noise discriminating variable) |
| Jet_hfcentralEtaStripSize | Int_t | eta size of the central tower strip in HF (noise discriminating variable) |
| Jet_hfsigmaEtaEta | Float_t | sigmaEtaEta for HF jets (noise discriminating variable) |
| Jet_hfsigmaPhiPhi | Float_t | sigmaPhiPhi for HF jets (noise discriminating variable) |
| Jet_jetId | Int_t | Jet ID flags bit1 is loose (always false in 2017 since it does not exist), bit2 is tight, bit3 is tightLepVeto |
| Jet_mass | Float_t | mass |
| Jet_muEF | Float_t | muon Energy Fraction |
| Jet_muonIdx1 | Int_t | (index to Muon) index of first matching muon |
| Jet_muonIdx2 | Int_t | (index to Muon) index of second matching muon |
| Jet_muonSubtrFactor | Float_t | 1-(muon-subtracted raw pt)/(raw pt) |
| Jet_nConstituents | UChar_t | Number of particles in the jet |
| Jet_nElectrons | Int_t | number of electrons in the jet |
| Jet_nMuons | Int_t | number of muons in the jet |
| Jet_neEmEF | Float_t | neutral Electromagnetic Energy Fraction |
| Jet_neHEF | Float_t | neutral Hadron Energy Fraction |
| Jet_phi | Float_t | phi |
| Jet_pt | Float_t | pt |
| Jet_puId | Int_t | Pileup ID flags with 106X (2016) training |
| Jet_puIdDisc | Float_t | Pileup ID discriminant with 106X (2016) training |
| Jet_qgl | Float_t | Quark vs Gluon likelihood discriminator |
| Jet_rawFactor | Float_t | 1 - Factor to get back to raw pT |
| nJet | UInt_t | slimmedJets, i.e. ak4 PFJets CHS with JECs applied, after basic selection (pt > 15) |
By now you should be able to identify the 4-vector information and the cross-reference indices in this list of branches! Many of the variables in the list will be discussed in the later lesson pages on heavy flavor tagging and jet energy corrections.
Jet identification
Particle-flow jets are not immune to noise in the detector, and jets used in analyses should be filtered to remove noise jets. CMS has defined a “noise jet ID” that considers information about the energy types within the jet:
- charged hadron fraction – what fraction of the jet consists of charged hadrons? This will be greater than 0 if the jet is within the inner tracker region.
- neutral hadron fraction – what fraction of the jet consists of neutral hadrons? This should always be less than 1.
- charged electromagnetic fraction – what fraction of the jet consists of electrons? This should always be less than 1.
- neutral electromagnetic fraction – what fraction of the jet consists of photons? This should always be less than 1.
- number of constituents – this should be greater than 1.
These criteria demonstrate how particle-flow jets combine information
across subdetectors. Jets will typically have energy from electrons and
photons, but those fractions of the total energy should be less than
one. Similarly, jets should have some energy from charged hadrons if
they overlap the inner tracker, and all the energy should not come from
neutral hadrons. A mixture of energy sources is expected for genuine
jets. All of these energy fractions (and more) can be accessed in
NanoAOD. Whenever you use jets, requirements should be placed on the
value of Jet_jetId, rejecting at least values of 0.
| Object property | Type | Description |
|---|---|---|
| Jet_chEmEF | Float_t | charged Electromagnetic Energy Fraction |
| Jet_chFPV0EF | Float_t | charged fromPV==0 Energy Fraction (energy excluded from CHS jets). Previously called betastar. |
| Jet_chHEF | Float_t | charged Hadron Energy Fraction |
| Jet_jetId | Int_t | Jet ID flags bit1 is loose (always false in 2017 since it does not exist), bit2 is tight, bit3 is tightLepVeto |
| Jet_muEF | Float_t | muon Energy Fraction |
| Jet_nConstituents | UChar_t | Number of particles in the jet |
| Jet_nElectrons | Int_t | number of electrons in the jet |
| Jet_nMuons | Int_t | number of muons in the jet |
| Jet_neEmEF | Float_t | neutral Electromagnetic Energy Fraction |
| Jet_neHEF | Float_t | neutral Hadron Energy Fraction |
| Jet_puId | Int_t | Pileup ID flags with 106X (2016) training |
Another important identification algorithm is the “pileup jet ID”, which can identify jets that are not likely to come from the primary collision of an event.
Large-radius jets in NanoAOD
Another useful anti-kt jet radius is 0.8, called “AK8 jets” or “large-radius jets”. These jets are stored if they have transverse momentum above 170 GeV, and are represented by the “FatJet_*” collection in NanoAOD:
| Object property | Type | Description |
|---|---|---|
| FatJet_area | Float_t | jet catchment area, for JECs |
| FatJet_btagCSVV2 | Float_t | pfCombinedInclusiveSecondaryVertexV2 b-tag discriminator (aka CSVV2) |
| FatJet_btagDDBvLV2 | Float_t | DeepDoubleX V2(mass-decorrelated) discriminator for H(Z)->bb vs QCD |
| FatJet_btagDDCvBV2 | Float_t | DeepDoubleX V2 (mass-decorrelated) discriminator for H(Z)->cc vs H(Z)->bb |
| FatJet_btagDDCvLV2 | Float_t | DeepDoubleX V2 (mass-decorrelated) discriminator for H(Z)->cc vs QCD |
| FatJet_btagDeepB | Float_t | DeepCSV b+bb tag discriminator |
| FatJet_btagHbb | Float_t | Higgs to BB tagger discriminator |
| FatJet_deepTagMD_H4qvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger H->4q vs QCD discriminator |
| FatJet_deepTagMD_HbbvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger H->bb vs QCD discriminator |
| FatJet_deepTagMD_TvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger top vs QCD discriminator |
| FatJet_deepTagMD_WvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger W vs QCD discriminator |
| FatJet_deepTagMD_ZHbbvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H->bb vs QCD discriminator |
| FatJet_deepTagMD_ZHccvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H->cc vs QCD discriminator |
| FatJet_deepTagMD_ZbbvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z->bb vs QCD discriminator |
| FatJet_deepTagMD_ZvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z vs QCD discriminator |
| FatJet_deepTagMD_bbvsLight | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H/gluon->bb vs light flavour discriminator |
| FatJet_deepTagMD_ccvsLight | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H/gluon->cc vs light flavour discriminator |
| FatJet_deepTag_H | Float_t | DeepBoostedJet tagger H(bb,cc,4q) sum |
| FatJet_deepTag_QCD | Float_t | DeepBoostedJet tagger QCD(bb,cc,b,c,others) sum |
| FatJet_deepTag_QCDothers | Float_t | DeepBoostedJet tagger QCDothers value |
| FatJet_deepTag_TvsQCD | Float_t | DeepBoostedJet tagger top vs QCD discriminator |
| FatJet_deepTag_WvsQCD | Float_t | DeepBoostedJet tagger W vs QCD discriminator |
| FatJet_deepTag_ZvsQCD | Float_t | DeepBoostedJet tagger Z vs QCD discriminator |
| FatJet_electronIdx3SJ | Int_t | (index to Electron) index of electron matched to jet |
| FatJet_eta | Float_t | eta |
| FatJet_jetId | Int_t | Jet ID flags bit1 is loose (always false in 2017 since it does not exist), bit2 is tight, bit3 is tightLepVeto |
| FatJet_lsf3 | Float_t | Lepton Subjet Fraction (3 subjets) |
| FatJet_mass | Float_t | mass |
| FatJet_msoftdrop | Float_t | Corrected soft drop mass with PUPPI |
| FatJet_muonIdx3SJ | Int_t | (index to Muon) index of muon matched to jet |
| FatJet_n2b1 | Float_t | N2 with beta=1 |
| FatJet_n3b1 | Float_t | N3 with beta=1 |
| FatJet_nConstituents | UChar_t | Number of particles in the jet |
| FatJet_particleNetMD_QCD | Float_t | Mass-decorrelated ParticleNet tagger raw QCD score |
| FatJet_particleNetMD_Xbb | Float_t | Mass-decorrelated ParticleNet tagger raw X->bb score. For X->bb vs QCD tagging, use Xbb/(Xbb+QCD) |
| FatJet_particleNetMD_Xcc | Float_t | Mass-decorrelated ParticleNet tagger raw X->cc score. For X->cc vs QCD tagging, use Xcc/(Xcc+QCD) |
| FatJet_particleNetMD_Xqq | Float_t | Mass-decorrelated ParticleNet tagger raw X->qq (uds) score. For X->qq vs QCD tagging, use Xqq/(Xqq+QCD). For W vs QCD tagging, use (Xcc+Xqq)/(Xcc+Xqq+QCD) |
| FatJet_particleNet_H4qvsQCD | Float_t | ParticleNet tagger H(->VV->qqqq) vs QCD discriminator |
| FatJet_particleNet_HbbvsQCD | Float_t | ParticleNet tagger H(->bb) vs QCD discriminator |
| FatJet_particleNet_HccvsQCD | Float_t | ParticleNet tagger H(->cc) vs QCD discriminator |
| FatJet_particleNet_QCD | Float_t | ParticleNet tagger QCD(bb,cc,b,c,others) sum |
| FatJet_particleNet_TvsQCD | Float_t | ParticleNet tagger top vs QCD discriminator |
| FatJet_particleNet_WvsQCD | Float_t | ParticleNet tagger W vs QCD discriminator |
| FatJet_particleNet_ZvsQCD | Float_t | ParticleNet tagger Z vs QCD discriminator |
| FatJet_particleNet_mass | Float_t | ParticleNet mass regression |
| FatJet_phi | Float_t | phi |
| FatJet_pt | Float_t | pt |
| FatJet_rawFactor | Float_t | 1 - Factor to get back to raw pT |
| FatJet_subJetIdx1 | Int_t | (index to Subjet) index of first subjet |
| FatJet_subJetIdx2 | Int_t | (index to Subjet) index of second subjet |
| FatJet_tau1 | Float_t | Nsubjettiness (1 axis) |
| FatJet_tau2 | Float_t | Nsubjettiness (2 axis) |
| FatJet_tau3 | Float_t | Nsubjettiness (3 axis) |
| FatJet_tau4 | Float_t | Nsubjettiness (4 axis) |
| nFatJet | UInt_t | slimmedJetsAK8, i.e. ak8 fat jets for boosted analysis |
Beyond the 4-vector information, FatJet_jetId variable,
and cross-reference indices, the overwhelming majority of variables
stored for FatJets are used to identify hadronic decays of high-momentum
massive SM particles like top quarks, Higgs bosons, W bosons, and Z
bosons. This will be covered in a later lesson.
MET
Missing transverse momentum is the negative vector sum of the transverse momenta of all particle flow candidates in an event. The magnitude of the missing transverse momentum vector is called missing transverse energy and referred to with the acronym “MET”. Since energy corrections are made to the particle flow jets (see the last page in this lesson), those corrections are propagated to MET by adding back the momentum vectors of the original jets and then subtracting the momentum vectors of the corrected jets. This correction is called “Type 1” and is standard for all CMS analyses.
| Object property | Type | Description |
|---|---|---|
| MET_MetUnclustEnUpDeltaX | Float_t | Delta (METx_mod-METx) Unclustered Energy Up |
| MET_MetUnclustEnUpDeltaY | Float_t | Delta (METy_mod-METy) Unclustered Energy Up |
| MET_covXX | Float_t | xx element of met covariance matrix |
| MET_covXY | Float_t | xy element of met covariance matrix |
| MET_covYY | Float_t | yy element of met covariance matrix |
| MET_phi | Float_t | phi |
| MET_pt | Float_t | pt |
| MET_significance | Float_t | MET significance |
| MET_sumEt | Float_t | scalar sum of Et |
| MET_sumPtUnclustered | Float_t | sumPt used for MET significance |
The standard “MET” magnitude is found in MET_pt, and the
azimuthal angle of the vector is MET_phi (since MET can
only be computed in the transverse plane, no MET_eta is
found). The MET_significance variable can be a useful tool:
it describes the likelihood that the MET arose from noise or
mismeasurement in the detector as opposed to a neutrino or similar
non-interacting particle. The four-vectors of the other physics objects
along with their uncertainties are required to compute the significance
of the MET signature. MET that is directed nearly (anti)colinnear with a
physics object is likely to arise from mismeasurement and should not
have a large significance.
Key Points
- Jets are spatially-grouped collections of particles that traversed the CMS detector
- Particles from additional proton-proton collisions (pileup) must be removed from jets
- Missing transverse energy is the negative vector sum of particle candidates
- Many of the variables discussed for other objects also exist for jets
Content from Jet flavor tagging
Last updated on 2024-07-09 | Edit this page
Overview
Questions
- How are b hadrons identified in CMS?
- How are the parent particles of large-radius jets identified in CMS?
Objectives
- Understand the basics of heavy flavor tagging
- Learn to access tagging information in NanoAOD files
Jet reconstruction and identification is an important part of the analyses at the LHC. A jet may contain the hadronization products of any quark or gluon, or possibly the decay products of more massive particles such as W or Higgs bosons. Several “b tagging” algorithms exist to identify jets from the hadronization of b quarks, which have unique properties that distinguish them from light quark or gluon jets.
B Tagging Algorithms
Tagging algorithms first connect the jets with good quality tracks that are either associated with one of the jet’s particle flow candidates or within a nearby cone. Both tracks and “secondary vertices” (track vertices from the decays of b hadrons) can be used in track-based, vertex-based, or “combined” tagging algorithms. The specific details depend upon the algorithm use. However, they all exploit properties of b hadrons such as:
- long lifetime,
- large mass,
- high track multiplicity,
- large semileptonic branching fraction,
- hard fragmentation fuction.
In CMS, several b tagging algorithms have existed over time:
- Track Counting: identifies a b jet if it contains at least N tracks with significantly non-zero impact parameters.
- Jet Probability: combines information from all selected tracks in the jet and uses probability density functions to assign a probability to each track
- Soft Muon and Soft Electron: identifies b jets by searching for a lepton from a semi-leptonic b decay.
- Simple Secondary Vertex: reconstructs the b decay vertex and calculates a discriminator using related kinematic variables.
- Combined Secondary Vertex (CSV): exploits all known kinematic variables of the jets, information about track impact parameter significance and the secondary vertices to distinguish b jets. This tagger became the default CMS algorithm in Run 1 and early Run 2.
- DeepCSV: the CSV algorithm was reimagined as a deep neural network.
- DeepJet: this deep neural network tagger uses a more complex architecture than DeepCSV, and is the most powerful b tagging algorithm for Run 2.
These algorithms produce a single, real number called a b tagging “discriminator” for each jet. The more positive the discriminator value, the more likely it is that this jet contained b hadrons. The DeepCSV and DeepJet algorithms can also identify charm-flavor jets, and DeepJet can even distinguish between light-quark and gluon jets.
| Object property | Type | Description |
|---|---|---|
| Jet_btagCSVV2 | Float_t | pfCombinedInclusiveSecondaryVertexV2 b-tag discriminator (aka CSVV2) |
| Jet_btagDeepB | Float_t | DeepCSV b+bb tag discriminator |
| Jet_btagDeepCvB | Float_t | DeepCSV c vs b+bb discriminator |
| Jet_btagDeepCvL | Float_t | DeepCSV c vs udsg discriminator |
| Jet_btagDeepFlavB | Float_t | DeepJet b+bb+lepb tag discriminator |
| Jet_btagDeepFlavCvB | Float_t | DeepJet c vs b+bb+lepb discriminator |
| Jet_btagDeepFlavCvL | Float_t | DeepJet c vs uds+g discriminator |
| Jet_btagDeepFlavQG | Float_t | DeepJet g vs uds discriminator |
Working points
A jet is considered “b tagged” if the discriminator value exceeds some threshold. Different thresholds will have different efficiencies for identifying true b quark jets and for mis-tagging light quark jets. As we saw for muons and other objects, a “loose” working point will allow the highest mis-tagging rate, while a “tight” working point will sacrifice some correct-tag efficiency to reduce mis-tagging. The DeepCSV and DeepJet algorithms are supported by CMS for 2016 Open Data.
The supported working points for DeepCSV and DeepJet for the 2016 Open Data are:
- Loose (10% misidentification rate):
Jet_btagDeepB> 0.1918 ,Jet_btagDeepFlav> 0.0480 - Medium (1% misidentification rate):
Jet_btagDeepB> 0.5847,Jet_btagDeepFlav> 0.2489 - Tight (0.1% misidentification rate):
Jet_btagDeepB> 0.8767,Jet_btagDeepFlav> 0.6377
The figure below shows the relationship between b jet efficiency and working point in DeepCSV and DeepJet:
FatJet tagging algorithms
Jets can originate from many different types of particles. The figure below gives an example of how different “parent particles” can influence the internal structure of a jet. Observables related to the mass and internal structure of a jet can help us design algorithms to distinguish between sources. The most common type of algorithm identifies b quark jets from light quark or gluon jets. The POET contains all the tools you need to evaluate the default CMS b tagging discriminants on small-radius jets. See the next episode for more information. In this lesson we will focus on tools to identify hadronic decays of Lorentz-boosed massive SM particles within large-radius jets.
Groomed mass and substructure
The mass of a jet is evaluated by summing the energy-momentum four-vectors of all the particle flow candidates that make up the jet and computing the mass of the resulting object. This mass calculation is distorted by the low-momentum and wide-angle gluon radiation emerging from the initial hadrons that formed the jet. For example, the masses of light quark or gluon jets are measured to be much larger than the actual masses of these particles – typically 10–50 GeV with a smooth continuum to higher values. Grooming procedures can help reduce the impact of this radiation and bring the jet mass closer to the true values of the parent particles. Grooming algorithms typically cluster the jet’s consitituents into “subjets”, like those represented by the small circles in the figure below. The relationships between different subjets can then be tested to decide which to keep.
The “softdrop” mass is included in NanoAOD for large-radius jets. In the “softdrop” procedure, jets are recursively de-clustered, and at each step jets that are too soft or at large angles are discarded. The following image shows the relationship between FatJet momentum, mass, and jet radius. As the momentum increases, jets of larger mass become contained within the FatJet. While W bosons can be observed from 200 GeV, top quarks require a higher momentum threshold.
The internal structure of a jet can be probed using many observables: N-subjettiness, energy correlation functions, and others. In CMS, N-subjettiness is the default jet substructure variable for identifying boosted particle decays.
The “tau” variables of N-subjettiness, defined below, are jet shape variables whose value approaches 0 for jets having N or fewer subjets:
\(\tau_{N} = \frac{\sum^{n_{\mathrm{constituents}}}_{i=1} p_{\mathrm{T},i} \min{\Delta R_{1,i}, \Delta R_{2,i}, \ldots, \Delta R_{N,i}}}{\sum^{n_{\mathrm{constituents}}}_{i=1} p_{T,i}R}\)
If the value approaches zero it indicates that the consitituents all lie near one of the previously identified subjet axes. For a top quark jet with 3 subjets, we would expect small tau values for N = 3, 4, 5, 6, etc, but larger values for N = 1 or 2. Ratios of tau values provide the best discrimination for jets with a specific number of subjets. For two-prong jets like W, Z, or H boson decays, we study the ratio tau_2 / tau_1. For three-prong jets we study tau_3 / tau_2.
The figures below show the relevant tau ratios for W boson (left) and top quark (right) jets. The structure in the tau_2/tau_1 plot is very unique: W bosons pool at lower values of tau_2/tau_1, while top quarks (with more than 2 subjets) and light quarks (with only 1 subjet) pool at medium and higher values. In the tau_3/tau_2 plot, top quark jets have low values while both W boson and light quark jets are gathered near 1.
|
For top quark or H boson decays, applying b tagging algorithms to the subjets of the large-radius jets gives another valuable substructure observable. The Combined Secondary Vertex v2 and the DeepCSV discriminants have been stored for the two subjets obtained from the soft drop algorithm in each large-radius jet. For simulation, we also store the generator-level flavor information for the subjet. You can explore the “Subjet” branches in NanoAOD here
Finally, NanoAOD contains some energy correlation function information for large-radius jets. The N2 and N3 functions are described in detail in a CMS paper on boosted jet identification.
Groomed mass, jet substructure, and subjet b-tagging were the backbone of early boosted jet identification in CMS. The figure below shows an example of isolating top quark jets by applying various mass and substructure criteria. However, these algorithms have now been eclipsed by deep neural network identification techniques.
| Object property | Type | Description |
|---|---|---|
| FatJet_msoftdrop | Float_t | Corrected soft drop mass with PUPPI |
| FatJet_n2b1 | Float_t | N2 with beta=1 |
| FatJet_n3b1 | Float_t | N3 with beta=1 |
| FatJet_subJetIdx1 | Int_t | (index to Subjet) index of first subjet |
| FatJet_subJetIdx2 | Int_t | (index to Subjet) index of second subjet |
| FatJet_tau1 | Float_t | Nsubjettiness (1 axis) |
| FatJet_tau2 | Float_t | Nsubjettiness (2 axis) |
| FatJet_tau3 | Float_t | Nsubjettiness (3 axis) |
| FatJet_tau4 | Float_t | Nsubjettiness (4 axis) |
Deep Neural Network taggers
During Run 2, CMS analysts developed many neural network identification schemes for large-radius jets. The best performers have been preserved in the version of NanoAOD available for Open Data. The main algorithms are:
- DeepDoubleX (or “double-b”): a Boosted Decision Tree optimized for decays of massive particles to a pair of b or c quarks.
- DeepBoostedJet (or “DeepAK8”): a Convolutional Neural Network combined with a dense network that uses particle-flow candidates and secondary vertices to determine the parent particle of the jet
- ParticleNet: a Dynamic Graph Convolutional Neural Network applied on “point cloud” data structures built from the particle-flow candidates within a jet.
The deep network taggers provide discriminants for many different particle hypotheses. These are typically grouped into “binarized” discriminants intended to separate a particular massive particle (top, Higgs, etc) from light quark jets. Both DeepAK8 and ParticleNet offer “mass-decorrelated” discriminants, for which the network has been trained in such a way that jet mass is not part of the learning process. For analyses that use the jet mass distribution as a key sensitive variable, decorrelation helps maintain a smoothly falling light-quark jet mass distribution, with no artificial peak near the region of interest (eg, near 125 GeV for Higgs bosons, or new 170 GeV for top quarks).
The branches available in NanoAOD for the deep network taggers are listed below.
| Object property | Type | Description |
|---|---|---|
| FatJet_btagDDBvLV2 | Float_t | DeepDoubleX V2(mass-decorrelated) discriminator for H(Z)->bb vs QCD |
| FatJet_btagDDCvBV2 | Float_t | DeepDoubleX V2 (mass-decorrelated) discriminator for H(Z)->cc vs H(Z)->bb |
| FatJet_btagDDCvLV2 | Float_t | DeepDoubleX V2 (mass-decorrelated) discriminator for H(Z)->cc vs QCD |
| FatJet_btagHbb | Float_t | Higgs to BB tagger discriminator |
| FatJet_deepTagMD_H4qvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger H->4q vs QCD discriminator |
| FatJet_deepTagMD_HbbvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger H->bb vs QCD discriminator |
| FatJet_deepTagMD_TvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger top vs QCD discriminator |
| FatJet_deepTagMD_WvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger W vs QCD discriminator |
| FatJet_deepTagMD_ZHbbvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H->bb vs QCD discriminator |
| FatJet_deepTagMD_ZHccvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H->cc vs QCD discriminator |
| FatJet_deepTagMD_ZbbvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z->bb vs QCD discriminator |
| FatJet_deepTagMD_ZvsQCD | Float_t | Mass-decorrelated DeepBoostedJet tagger Z vs QCD discriminator |
| FatJet_deepTagMD_bbvsLight | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H/gluon->bb vs light flavour discriminator |
| FatJet_deepTagMD_ccvsLight | Float_t | Mass-decorrelated DeepBoostedJet tagger Z/H/gluon->cc vs light flavour discriminator |
| FatJet_deepTag_H | Float_t | DeepBoostedJet tagger H(bb,cc,4q) sum |
| FatJet_deepTag_QCD | Float_t | DeepBoostedJet tagger QCD(bb,cc,b,c,others) sum |
| FatJet_deepTag_QCDothers | Float_t | DeepBoostedJet tagger QCDothers value |
| FatJet_deepTag_TvsQCD | Float_t | DeepBoostedJet tagger top vs QCD discriminator |
| FatJet_deepTag_WvsQCD | Float_t | DeepBoostedJet tagger W vs QCD discriminator |
| FatJet_deepTag_ZvsQCD | Float_t | DeepBoostedJet tagger Z vs QCD discriminator |
| FatJet_particleNetMD_QCD | Float_t | Mass-decorrelated ParticleNet tagger raw QCD score |
| FatJet_particleNetMD_Xbb | Float_t | Mass-decorrelated ParticleNet tagger raw X->bb score. For X->bb vs QCD tagging, use Xbb/(Xbb+QCD) |
| FatJet_particleNetMD_Xcc | Float_t | Mass-decorrelated ParticleNet tagger raw X->cc score. For X->cc vs QCD tagging, use Xcc/(Xcc+QCD) |
| FatJet_particleNetMD_Xqq | Float_t | Mass-decorrelated ParticleNet tagger raw X->qq (uds) score. For X->qq vs QCD tagging, use Xqq/(Xqq+QCD). For W vs QCD tagging, use (Xcc+Xqq)/(Xcc+Xqq+QCD) |
| FatJet_particleNet_H4qvsQCD | Float_t | ParticleNet tagger H(->VV->qqqq) vs QCD discriminator |
| FatJet_particleNet_HbbvsQCD | Float_t | ParticleNet tagger H(->bb) vs QCD discriminator |
| FatJet_particleNet_HccvsQCD | Float_t | ParticleNet tagger H(->cc) vs QCD discriminator |
| FatJet_particleNet_QCD | Float_t | ParticleNet tagger QCD(bb,cc,b,c,others) sum |
| FatJet_particleNet_TvsQCD | Float_t | ParticleNet tagger top vs QCD discriminator |
| FatJet_particleNet_WvsQCD | Float_t | ParticleNet tagger W vs QCD discriminator |
| FatJet_particleNet_ZvsQCD | Float_t | ParticleNet tagger Z vs QCD discriminator |
| FatJet_particleNet_mass | Float_t | ParticleNet mass regression |
Tagger scale factors
Scale factors to increase or decrease the number of tagged jets in simulation can be applied in a number of ways, but typically involve weighting simulation events based on the efficiencies and scale factors relevant to each jet in the event.
For small-radius jet b-tagging, details and usage references from Run 1 can be found at these references. The concepts and methods for applying scale factors are unchanged in Run 2.
The most common scale factor application method (1a) relies on 4
pieces of information for each jet in simulation: * Tagging status: does
this jet pass the discriminator threshold for a given working point? *
Flavor (b, c, light): accessed using a pat::Jet member
function called partonFlavour(). * Efficiency: measured as
a function of momentum as in the image above. * Scale factor: accessed
from the
For large-radius jet tagging, scale factors are computed for specific boosted particle flavors and can be applied using similar methods as for b tagging.
Spplication instructions coming soon!
The CMS Open Data Guide will include the scale factor data files and application instructions for 2015 and 2016 Open Data.
Key Points
- Tagging algorithms separate heavy flavor jets from jets produced by the hadronization of light quarks and gluons
- FatJet tagging algorithms can identify jets from massive SM particles
- Tagging algorithms produce a disriminator value for each jet that represents the likelihood that the jet came from a particular particle
- Each tagging algorithm has recommended ‘working points’ (discriminator values) based on a misidentification probability for non-interesting jets
Content from Jet corrections
Last updated on 2024-07-24 | Edit this page
Overview
Questions
- How are data/simulation differences dealt with for jet energy?
- How do uncorrected and corrected jet momenta compare?
- How large is the JES uncertainty in different regions?
- How large is the JER uncertainty in different regions?
Objectives
- Learn about typical differences in jet energy scale and resolution between data and simulation
- Explore the JES and JER uncertainties using histograms
Unsurprisingly, the CMS detector does not measure jet energies perfectly, nor do simulation and data agree perfectly! The measured energy of jet must be corrected so that it can be related to the true energy of its parent particle. These “Jet Energy Scale” (JES) corrections account for several effects and are factorized so that each effect can be studied independently. All of the corrections in this section are described in “Jet Energy Scale and Resolution” papers by CMS: * 2011, 7 TeV * 2017, 8 TeV
JES Correction levels
Particles from additional interactions in nearby bunch crossings of the LHC contribute energy in the calorimeters that must somehow be distinguished from the energy deposits of the main interaction. Extra energy in a jet’s cone can make its measured momentum larger than the momentum of the parent particle. The first layer (“L1”) of jet energy corrections accounts for pileup by subtracting the average transverse momentum contribution of the pileup interactions to the jet’s cone area. This average pileup contribution varies by pseudorapidity and, of course, by the number of interactions in the event.
The second and third layers of corrections (“L2L3”) correct the measured momentum to the true momentum as functions of momentum and pseudorapidity, bringing the reconstructed jet in line with the generated jet. These corrections are derived using momentum balancing and missing energy techniques in dijet and Z boson events. One well-measured object (ex: a jet near the center of the detector, a Z boson reconstructed from leptons) is balanced against a jet for which corrections are derived.
All of these corrections are applied to both data and simulation. Data events are then given “residual” corrections to bring data into line with the corrected simulation. A final set of flavor-based corrections are used in certain analyses that are especially sensitive to flavor effects. The figure below shows the result of the L1+L2+L3 corrections on the jet response.
Jet Energy Resolution
Jet Energy Resolution (JER) corrections are applied after JES on strictly MC simulations. Unlike JES, which adjusts the mean of the momentun response distribution, JER adjusts the width of the distribution. The ratio of reconstructed transverse momentum to true (generated) transverse momentum forms a Gaussian distributions – the width of this Gaussian is the JER. In data, where no “true” pT is available, the JER is measured using photon/Z + jet events where the jet recoils against the photon or Z boson, both of which can be measured quite precisely in the CMS detector. The JER is typically smaller in simulation than in data, leading to scale factors that are larger than 1. These scale factors are applied using two methods:
- Adjusting the ratio of reconstructed to generated momentum using the scale factor (if a well-matched generated jet is found),
- Randomly smearing the momentum using a Gaussian distribution based on the resolution and scale factor (if no generated jet is found).
Applying JES and JER
Earlier editions of this workshop documented a long process of applying the appropriate corrections to MiniAOD Open Data for 2015! The 2016 Open Data samples are “Ultra Legacy”, and an appropriate set of corrections have already been applied to the jets.
Application instructions coming soon!
Sometimes, you may need to reapply the jet corrections in an analysis, perhaps after removing leptons from jets. Instructions and examples to perform this process with NanoAOD samples will be included in the CMS Open Data Guide later in 2024.
Uncertainties
All corrections have accompanying uncertainties. The JES uncertainties have several sources, shown in the figure below. The L1 (pileup) uncertainty dominates at low momentum, while the L3 (absolute scale) uncertainty takes over for higher momentum jets. All corrections are quite precise for jets located near the center of the CMS barrel region, and the precision drops as pseudorapidity increases and different subdetectors lose coverage.
The JER uncertainty is evaluated by shifting the scale factors up and down according to the error bars shown in the scale factor figure above. These uncertainties arise from treatment of initial and final state radiation in the data measurement, differences in Monte Carlo tunes across generator platforms, and small non-Gaussian tail effects. The JER uncertainty is evaluated by re-calculating the smearing factor using the shifted scale factors. The uncertainties in JES and JER are kept separate from each other: when varying JES, the JER correction is held constant, and vice versa. This results in 5 momentum values for each jet: a central value and two sets of uncertainties:
The JES corrections are significant, far larger than the uncertainty itself. The first level of correction, for pileup removal, tends to reduce the momentum of the jet, as seen in the left figure below that compares corrected to uncorrected jets. The right figure shows a similar comparison for JER smearing – this uncertainty is much smaller for the majority of jets!
|
It is useful to make the same comparisons for jets in the forward regions of the CMS detector, where tracking is not available. The left (right) figure below shows JES (JER) effects for jets with pseudorapidity greater than 3.
|
In the endcap region the uncertainty on the JER scale factor has
become nearly 20%! So this uncertainty gains almost equal footing with
JES. Many CMS analyses restrict themselves to studying jets in the
“central” region of the detector, defined loosely by the tracker
acceptance region of abs(eta) < 2.4 precisely to avoid
these larger JES and JER uncertainties.
Uncertainty instructions coming soon!
Methods to evaluate JES and JER uncertainties for NanoAOD files will also be included in the CMS Open Data Guide later in 2024.
Key Points
- Jet energy corrections are factorized and account for many mismeasurement effects
- L1+L2+L3 should be applied to jets used for analyses, with residual corrections for data
- Jet energy resolution in simulation is typically too narrow and is smeared using scale factors
- Jet energy and resolution corrections are sources of systematic error and uncertainties should be evaluated
- In general, the jet corrections are significant and lower the momenta of the jets with standard LHC pileup conditions
- For most jets, the JES uncertainty dominates over the JER uncertainty
- In the endcap region of the detector, the JER uncertainty in larger and matches the JES uncertainty
