Electrons

Overview

Teaching: 10 min
Exercises: 30 min

Questions

• What are electromagnetic objects

• How are electrons treated in CMS?

• What variable are available using POET?

• How can one add a new electron variable?

Objectives

• Understand what electromagnetic objects are in CMS

• Learn electron member functions for common track-based quantities

• Learn member functions for identification and isolation of electrons

• Learn member functions for electron detector-related quantities

• Learn how to add new information to the EDAnalyzer

Prerequisites

• We will be still running on the CMSSW Docker container. If you closed it for some reason, just fire it back up.
• During the last episode we made modifications to our python/poet_cfg.py file. If for some reason yours got into an invalid state, just copy/paste from the last episode.

Motivation

In the middle of the workshop we will be working on the main activity, which is to attempt to replicate a CMS physics analysis in a simplified way using modern analysis tools. The final state that we will be looking at contains electrons, muons and jets. We are using these objects as examples to review the way in which we extract physics objects information.

The analysis requires some special variables, which we will have to figure out how to implement.

Electromagnetic objects

We call photons and electrons electromagnetic particles because they leave most of their energy in the electromagnetic calorimeter (ECAL) so they share many common properties and functions

Many of the different hypothetical exotic particles are unstable and can transform, or decay, into electrons, photons, or both. Electrons and photons are also standard tools to measure better and understand the properties of already known particles. For example, one way to find a Higgs Boson is by looking for signs of two photons, or four electrons in the debris of high energy collisions. Because electrons and photons are crucial in so many different scenarios, the physicists in the CMS collaboration make sure to do their best to reconstruct and identify these objects.

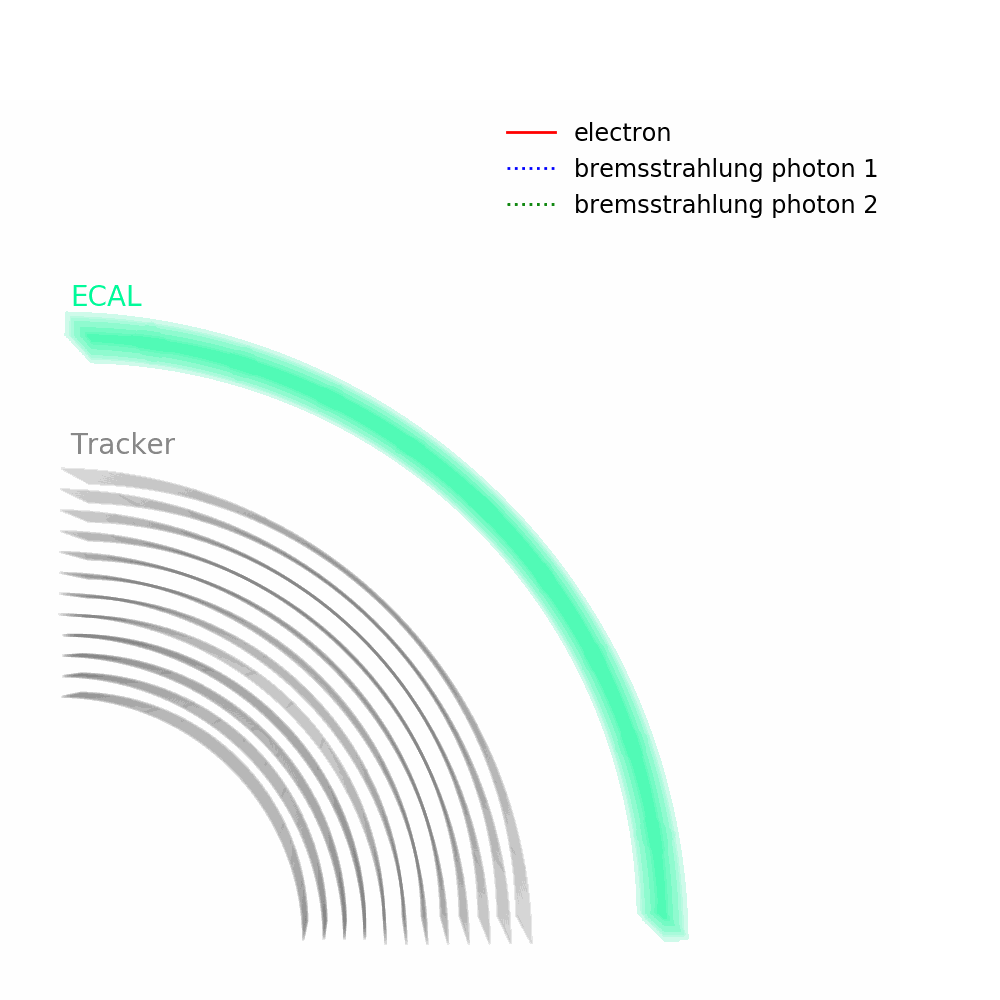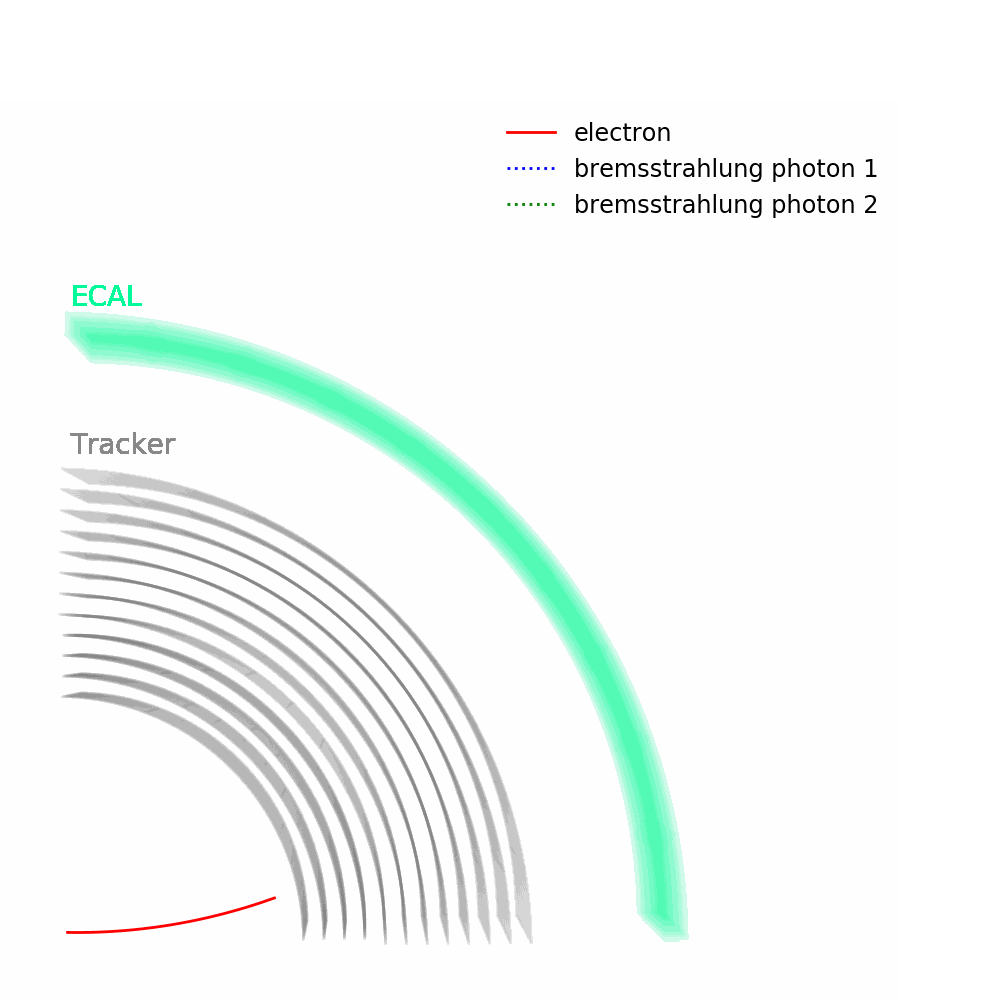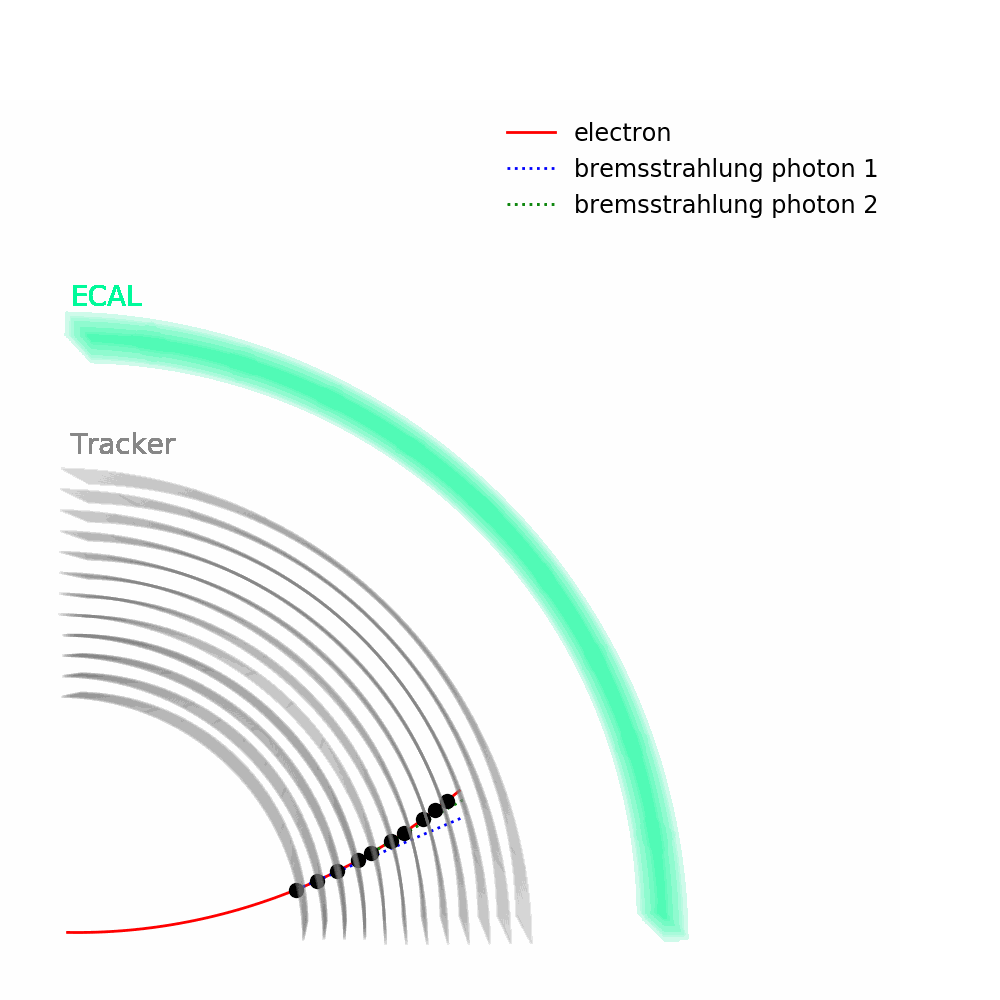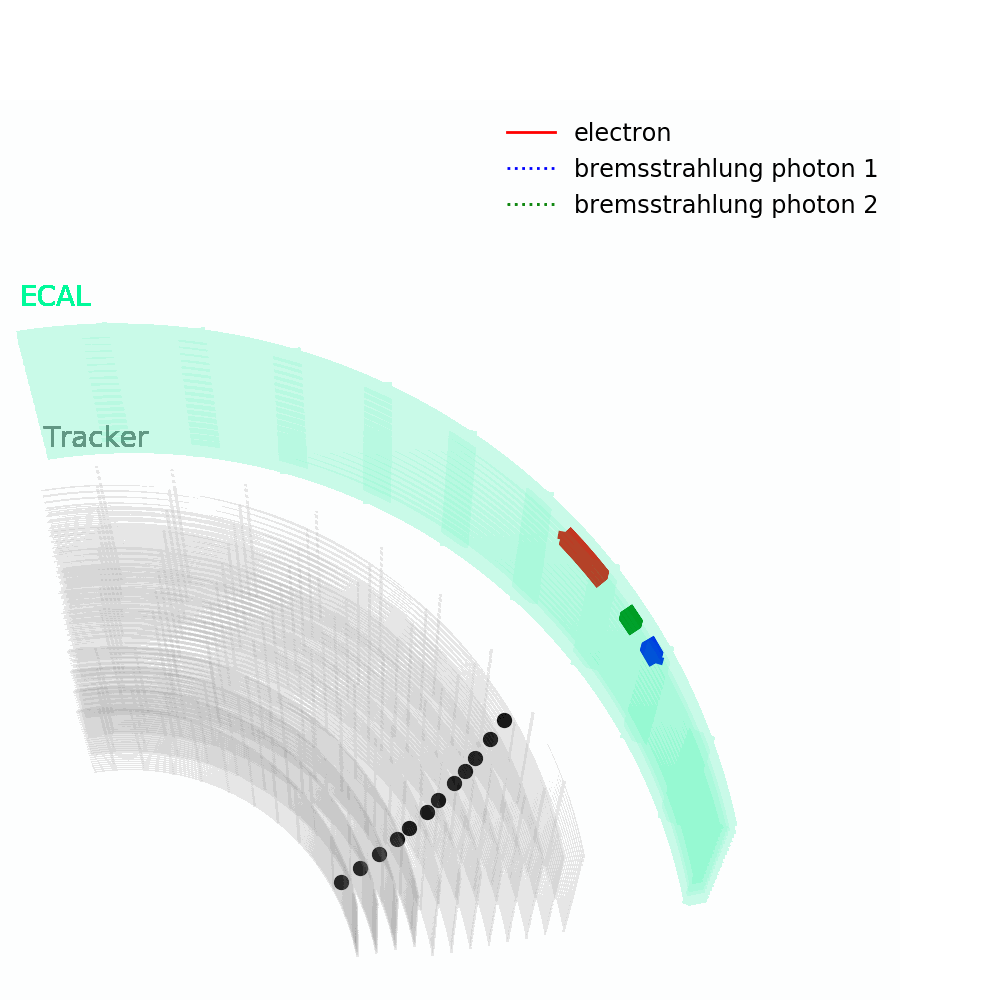
As depicted in the figure above, tracks – from the pixel and silicon tracker systems – as well as ECAL energy deposits are used to identify the passage of electrons in CMS. Being charged, electron trajectories curve inside the CMS magnetic field. Photons are similar objects but with no tracks. Sophisticated algorithms are run in the reconstruction to take into account subtleties related to the identification of an electromagnetic particle. An example is the convoluted showering of sub-photons and sub-electrons that can reach the ECAL due to bremsstrahlung and photon conversions.

We measure momentum and energy but also other properties of these objects that help analysts understand better their quality and origin. Let’s explore the ElectronAnalyzer in POET to get a sense of some of these properties.

The ElectronAnalyzer.cc EDAnalyzer

Fire up your favorite editor on your local machine and open the src/ElectronAnalyzer.cc file from the PhysObjectExtractorTool/PhysObjectExtractor package of your curent POET repository.

Needed libraries

The first thing that you will see is a set of includes. In particular we have a set of headers for electrons:

...
//class to extract electron information
#include "DataFormats/PatCandidates/interface/Electron.h"
#include "DataFormats/EgammaCandidates/interface/GsfElectron.h"
#include "DataFormats/VertexReco/interface/VertexFwd.h"
#include "DataFormats/VertexReco/interface/Vertex.h"
...

Electron 4-vector and track information

In the loop over the electron collection in ElectronAnalyzer.cc, we access elements of the four-vector as shown in the last episode:

for (const pat::Electron &el : *electrons){
    ...
    electron_e.push_back(el.energy());
    electron_pt.push_back(el.pt());
    ...
}

Most charged physics objects are also connected to tracks from the CMS tracking detectors. The charge of the object can be queried directly:

electron_ch.push_back(el.charge());

Information from tracks provides other kinematic quantities that are common to multiple types of objects. Often, the most pertinent information about an object to access from its associated track is its impact parameter with respect to the primary interaction vertex. We can access the impact parameters in the xy-plane (dxy or d0) and along the beam axis (dz), as well as their respective uncertainties.

math::XYZPoint pv(vertices->begin()->position());
...

electron_dxy.push_back(el.gsfTrack()->dxy(pv));
electron_dz.push_back(el.gsfTrack()->dz(pv));
electron_dxyError.push_back(el.gsfTrack()->d0Error());
electron_dzError.push_back(el.gsfTrack()->dzError());

Note: in the case of Photons, since they are neutral objects, they do not have a direct track link (though displaced track segments may appear from electrons or positrons produced by the photon as it transits the detector material). While the charge() method exists for all objects, it is not used in photon analyses.

Detector information for identification

The most signicant difference between a list of certain particles from a Monte Carlo generator and a list of the corresponding physics objects from CMS is likely the inherent uncertainty in the reconstruction. Selection of “a muon” or “an electron” for analysis requires algorithms designed to separate “real” objects from “fakes”. These are called identification algorithms.

Other algorithms are designed to measure the amount of energy deposited near the object, to determine if it was likely produced near the primary interaction (typically little nearby energy), or from the decay of a longer-lived particle (typically a lot of nearby energy). These are called isolation algorithms. Many types of isolation algorithms exist to deal with unique physics cases!

Both types of algorithms function using working points that are described on a spectrum from “loose” to “tight”. Working points that are “looser” tend to have a high efficiency for accepting real objects, but perhaps a poor rejection rate for “fake” objects. Working points that are “tighter” tend to have lower efficiencies for accepting real objects, but much better rejection rates for “fake” objects. The choice of working point is highly analysis dependent! Some analyses value efficiency over background rejection, and some analyses are the opposite.

The standard identification and isolation algorithm results can be accessed from the physics object classes.

Multivariate Electron Identification (MVA)

In the Multi-variate Analysis (MVA) approach, one forms a single discriminator variable that is computed based on multiple parameters of the electron object and provides the best separation between the signal and backgrounds by means of multivariate analysis methods and statistical learning tools. One can then cut on discriminator value or use the distribution of the values for a shape based statistical analysis.

There are two basic types of MVAs that are were trained by CMS for 2015 MiniAOD electrons:

• the triggering MVA: the discriminator is trained on the electrons that pass typical electron trigger requirements
• the non-triggering MVA: the discriminator is trained on all electrons regardless of the trigger

As an example in the ElectronAnalyzer we use the non-triggering MVA. Note that the tags used are ...wp90 and ...wp80. As mentioned above, the difference lies on the working point (wp). Both 80% and 90% are the signal efficiency for each MVA category as measured on electron.

      electron_ismvaLoose.push_back(el.electronID("mvaEleID-Spring15-25ns-nonTrig-V1-wp90"));
      electron_ismvaTight.push_back(el.electronID("mvaEleID-Spring15-25ns-nonTrig-V1-wp80"));

The MVA training provides working points with decreased electron fake rate.

Cut Based Electron ID

Electron identification can also be evaluated without MVAs, using a set of “cut-based” identification criteria:

...
      electron_veto.push_back(el.electronID("cutBasedElectronID-Spring15-25ns-V1-standalone-veto"));//
      electron_isLoose.push_back(el.electronID("cutBasedElectronID-Spring15-25ns-V1-standalone-loose"));
      electron_isMedium.push_back(el.electronID("cutBasedElectronID-Spring15-25ns-V1-standalone-medium"));
      electron_isTight.push_back(el.electronID("cutBasedElectronID-Spring15-25ns-V1-standalone-tight"));
...

Let’s break down these criteria:

• cutBasedElectronID...veto is a tag that rejects electrons coming from photon conversions in the tracker, which should instead be reconstructed as part of the photon.

Four standard working points are provided

• Veto (average efficiency ~95%). Use this working point for third lepton veto or counting.
• Loose (average efficiency ~90%). Use this working point when backgrounds are rather low.
• Medium (average efficiency ~80%). This is a good starting point for generic measurements involving W or Z bosons.
• Tight (average efficiency ~70%). Use this working point for measurements where backgrounds are a serious problem.

Isolation is computed in similar ways for all physics objects: search for particles in a cone around the object of interest and sum up their energies, subtracting off the energy deposited by pileup particles. This sum divided by the object of interest’s transverse momentum is called relative isolation and is the most common way to determine whether an object was produced “promptly” in or following the proton-proton collision (ex: electrons from a Z boson decay, or photons from a Higgs boson decay). Relative isolation values will tend to be large for particles that emerged from weak decays of hadrons within jets, or other similar “nonprompt” processes. For electrons, isolation is computed as:

...
electron_iso.push_back(el.ecalPFClusterIso());
...

Note: these POET implementations of identification working points are appropriate for 2015 data analysis.

Electron impact parameter variables

If you read the article mentioned above, which we would like to partially reproduce, you would encounter the usage of a variable which is described as:

Nonprompt leptons that come from the decays of long-lived hadrons are rejected by requiring that the significance of the three-dimensional (3D) impact parameter of the lepton track, relative to the primary event vertex, is less than four standard deviations. This requirement effectively reduces the contamination from multijet events, while keeping a high efficiency for the signal

Can you find this (spi3d) variable in the ElectronAnalyzer code? …

As it turns out, implementing the ip3d variable is very simple because it is already availabe as an accessible method in the class we use to access basically everything.
However, its partner sip3d is not simple to implement.

There is an alternative way of accesing this ip3d variable, as you can see here. We would be, essentially, recomputing this variable out of transient tracks. We can build transient tracks from our electron’s track, which is easily accessible as you could note here.

What the code snippet above tells us is that the significance should come from an C++ object created by the IPTools class. Exploring that class you will find the appropriate C++ object and how to retrieve it.

The C++ object name will naturally point you to the class to look at in the header of the IPTools class. Once you find it, you will be able to identify the needed method for extracting the significance.

Whew! Implementing code for new detector-related variables is an exercise in C++ class reference searching! If you were implementing this from scratch you would have needed to:

• Add two vectors:

  std::vector<double> electron_ip3d;	
  std::vector<double> electron_sip3d;
  

• Add two branches to the output tree:

  mtree->Branch("electron_ip3d",&electron_ip3d);
  mtree->GetBranch("electron_ip3d")->SetTitle("electron impact parameter in 3d");
  mtree->Branch("electron_sip3d",&electron_sip3d);
  mtree->GetBranch("electron_sip3d")->SetTitle("electron significance on impact parameter in 3d");
  

• Clear the vectors before processing each event: Vector clearing:

  electron_ip3d.clear();
  electron_sip3d.clear();
  

• Build transient tracks and compute the sip3d variables as instructed in the Software Guide (near the bottom of the analyze function): ~~~ electron_ismvaTight.push_back(el.electronID(“mvaEleID-Spring15-25ns-nonTrig-V1-wp80”));

edm::ESHandle trackBuilder; iSetup.get().get("TransientTrackBuilder", trackBuilder); reco::TransientTrack tt = trackBuilder->build(el.gsfTrack()); std::pair<bool,Measurement1D> ip3dpv = IPTools::absoluteImpactParameter3D(tt, primaryVertex); electron_ip3d.push_back(ip3dpv.second.value()); electron_sip3d.push_back(ip3dpv.second.significance());

numelectron++; ~~~

• Add the TransientTrack and IPTools libraries to the BuildFile.xml of the package.

The end!

Photons

Since photons are also primarily reconstructed as electromagnetic calorimeter showers, the vast majority of their reconstruction methods are common with electrons. The PhotonAnalyzer.cc file contains representative photon information, including identification working points. Extra information can be found from the 2015 MiniAOD Workbook page.

Key Points

• Quantities such as impact parameters and charge have common member functions.

• Physics objects in CMS are reconstructed from detector signals and are never 100% certain!

• Identification and isolation algorithms are important for reducing fake objects.

• One can add additional informtion to the EDAnalyzer