Introduction
Overview
Teaching: 20 min
Exercises: 20 minQuestions
What analysis will we be doing?
What is columnar analysis?
Why do we use coffea?
What are coffea main components?
What are schemas?
Objectives
Learn about the strategy we will follow for our analysis example.
Learn what the difference is between columnar and loop analysis.
Learn what coffea is and what the logic is of its different compoonets
Learn about what schemas are used for and how to modify them
Prerequisites
In order to use the
coffeaframework for our analysis, we need to install these additional packages directly in our container. We are addingcabinetryas well because we will use it later in our last episode.pip install vector hist mplhep coffea cabinetryAlso, download this file, which is our starting schema. Directly in your
/codearea (or locally in yourcms_open_data_pythondirectory) you can simply do:wget https://raw.githubusercontent.com/cms-opendata-workshop/workshop2022-lesson-ttbarljetsanalysis-payload/master/trunk/agc_schema.py
Introduction
In this simplified analysis we will be working towards a measurement of the top and anti-top quark production cross section \(\sigma_{t\bar{t}}\). The data are produced in proton-proton collisions at \(\sqrt{s}\) = 13 TeV at the beginning of Run 2 of the LHC. We will be examining the lepton+jets final state \(t\bar{t} \rightarrow (bW^{+})(\bar{b}W_{-}) \rightarrow bq\bar{q} bl^{-}\bar{\nu_{l}}\) which is characterized by one lepton (here we look at electrons and muons only), significant missing transverse energy, and four jets, two of which are identified as b-jets.
We will attempt to use tools that are built on modern, powerful and efficient python ecosystems. In particular, we will use the Columnar Object Framework For Effective Analysis (Coffea), which will provide us with basic tools and wrappers for enabling not-too-alien syntax when running columnar Collider HEP analysis.
Before we begin, let us mention that we will run these commands in a jupyter notebook, which can be started in the python container as
jupyter-lab --ip=0.0.0.0 --no-browserYou can look at the prompt and get the right link to paste in your browser.
You are welcome to do that as well or just follow along in python, interactively, i.e., start python as
pythonand input the commands in the command line.
Columnar analysis basics with Awkward
Note: this and the next section on this episode are a recast (with some shameless copying and pasting) of this notebook by Mat Adamec presented during the IRIS-HEP AGC Workshop 2022.
In one of the pre-exercises we learned how to access ROOT files (the standard use at the LHC experiments) using uproot and why the awkward library can be very helpufl when dealing with jagged arrays.
Let’s remember very quickly. First, be sure to import the appropriate libraries:
import uproot
import awkward as ak
Let’s open an example file. These are flattened POET ntuples. As it was mentioned in the trigger lesson, we will be producing these skimmed ntuples for you. You may recognize all the variables we had worked with before.
Using uproot,
events = uproot.open('root://eospublic.cern.ch//eos/opendata/cms/upload/od-workshop/ws2021/myoutput_odws2022-ttbaljets-prodv2.0_merged.root')['events']
events
<TTree 'events' (275 branches) at 0x7fb46a8b5870>.
We now have an events tree. We can view its branches by querying its keys():
events.keys()
['numberelectron', 'nelectron_e', 'electron_e', 'nelectron_pt', 'electron_pt', 'nelectron_px', 'electron_px', 'nelectron_py', 'electron_py', 'nelectron_pz', 'electron_pz', 'nelectron_eta', 'electron_eta', 'nelectron_phi', 'electron_phi', 'nelectron_ch', 'electron_ch', 'nelectron_iso', 'electron_iso', 'nelectron_veto', 'electron_veto', 'nelectron_isLoose', 'electron_isLoose', 'nelectron_isMedium', 'electron_isMedium', 'nelectron_isTight', 'electron_isTight', 'nelectron_dxy', 'electron_dxy', 'nelectron_dz', 'electron_dz', 'nelectron_dxyError', 'electron_dxyError', 'nelectron_dzError', 'electron_dzError', 'nelectron_ismvaLoose', 'electron_ismvaLoose', 'nelectron_ismvaTight', 'electron_ismvaTight', 'nelectron_ip3d', 'electron_ip3d', 'nelectron_sip3d', 'electron_sip3d', 'numberfatjet', 'nfatjet_e', 'fatjet_e', 'nfatjet_pt', 'fatjet_pt', 'nfatjet_eta', 'fatjet_eta', 'nfatjet_phi', 'fatjet_phi', 'nfatjet_ch', 'fatjet_ch', 'nfatjet_mass', 'fatjet_mass', 'nfatjet_corrpt', 'fatjet_corrpt', 'nfatjet_corrptUp', 'fatjet_corrptUp', 'nfatjet_corrptDown', 'fatjet_corrptDown', 'nfatjet_corrptSmearUp', 'fatjet_corrptSmearUp', 'nfatjet_corrptSmearDown', 'fatjet_corrptSmearDown', 'nfatjet_corrmass', 'fatjet_corrmass', 'nfatjet_corre', 'fatjet_corre', 'nfatjet_corrpx', 'fatjet_corrpx', 'nfatjet_corrpy', 'fatjet_corrpy', 'nfatjet_corrpz', 'fatjet_corrpz', 'nfatjet_prunedmass', 'fatjet_prunedmass', 'nfatjet_softdropmass', 'fatjet_softdropmass', 'nfatjet_tau1', 'fatjet_tau1', 'nfatjet_tau2', 'fatjet_tau2', 'nfatjet_tau3', 'fatjet_tau3', 'nfatjet_subjet1btag', 'fatjet_subjet1btag', 'nfatjet_subjet2btag', 'fatjet_subjet2btag', 'nfatjet_subjet1hflav', 'fatjet_subjet1hflav', 'nfatjet_subjet2hflav', 'fatjet_subjet2hflav', 'numberjet', 'njet_e', 'jet_e', 'njet_pt', 'jet_pt', 'njet_eta', 'jet_eta', 'njet_phi', 'jet_phi', 'njet_ch', 'jet_ch', 'njet_mass', 'jet_mass', 'njet_btag', 'jet_btag', 'njet_hflav', 'jet_hflav', 'njet_corrpt', 'jet_corrpt', 'njet_corrptUp', 'jet_corrptUp', 'njet_corrptDown', 'jet_corrptDown', 'njet_corrptSmearUp', 'jet_corrptSmearUp', 'njet_corrptSmearDown', 'jet_corrptSmearDown', 'njet_corrmass', 'jet_corrmass', 'njet_corre', 'jet_corre', 'njet_corrpx', 'jet_corrpx', 'njet_corrpy', 'jet_corrpy', 'njet_corrpz', 'jet_corrpz', 'btag_Weight', 'btag_WeightUp', 'btag_WeightDn', 'met_e', 'met_pt', 'met_px', 'met_py', 'met_phi', 'met_significance', 'met_rawpt', 'met_rawphi', 'met_rawe', 'numbermuon', 'nmuon_e', 'muon_e', 'nmuon_pt', 'muon_pt', 'nmuon_px', 'muon_px', 'nmuon_py', 'muon_py', 'nmuon_pz', 'muon_pz', 'nmuon_eta', 'muon_eta', 'nmuon_phi', 'muon_phi', 'nmuon_ch', 'muon_ch', 'nmuon_isLoose', 'muon_isLoose', 'nmuon_isMedium', 'muon_isMedium', 'nmuon_isTight', 'muon_isTight', 'nmuon_isSoft', 'muon_isSoft', 'nmuon_isHighPt', 'muon_isHighPt', 'nmuon_dxy', 'muon_dxy', 'nmuon_dz', 'muon_dz', 'nmuon_dxyError', 'muon_dxyError', 'nmuon_dzError', 'muon_dzError', 'nmuon_pfreliso03all', 'muon_pfreliso03all', 'nmuon_pfreliso04all', 'muon_pfreliso04all', 'nmuon_pfreliso04DBCorr', 'muon_pfreliso04DBCorr', 'nmuon_TkIso03', 'muon_TkIso03', 'nmuon_jetidx', 'muon_jetidx', 'nmuon_genpartidx', 'muon_genpartidx', 'nmuon_ip3d', 'muon_ip3d', 'nmuon_sip3d', 'muon_sip3d', 'numberphoton', 'nphoton_e', 'photon_e', 'nphoton_pt', 'photon_pt', 'nphoton_px', 'photon_px', 'nphoton_py', 'photon_py', 'nphoton_pz', 'photon_pz', 'nphoton_eta', 'photon_eta', 'nphoton_phi', 'photon_phi', 'nphoton_ch', 'photon_ch', 'nphoton_chIso', 'photon_chIso', 'nphoton_nhIso', 'photon_nhIso', 'nphoton_phIso', 'photon_phIso', 'nphoton_isLoose', 'photon_isLoose', 'nphoton_isMedium', 'photon_isMedium', 'nphoton_isTight', 'photon_isTight', 'nPV_chi2', 'PV_chi2', 'nPV_ndof', 'PV_ndof', 'PV_npvs', 'PV_npvsGood', 'nPV_x', 'PV_x', 'nPV_y', 'PV_y', 'nPV_z', 'PV_z', 'trig_Ele22_eta2p1_WPLoose_Gsf', 'trig_IsoMu20', 'trig_IsoTkMu20', 'numbertau', 'ntau_e', 'tau_e', 'ntau_pt', 'tau_pt', 'ntau_px', 'tau_px', 'ntau_py', 'tau_py', 'ntau_pz', 'tau_pz', 'ntau_eta', 'tau_eta', 'ntau_phi', 'tau_phi', 'ntau_ch', 'tau_ch', 'ntau_mass', 'tau_mass', 'ntau_decaymode', 'tau_decaymode', 'ntau_iddecaymode', 'tau_iddecaymode', 'ntau_idisoraw', 'tau_idisoraw', 'ntau_idisovloose', 'tau_idisovloose', 'ntau_idisoloose', 'tau_idisoloose', 'ntau_idisomedium', 'tau_idisomedium', 'ntau_idisotight', 'tau_idisotight', 'ntau_idantieletight', 'tau_idantieletight', 'ntau_idantimutight', 'tau_idantimutight']
Each of these branches can be interpreted as an awkward array. Let’s examine their contents to remember that they contain jagged (non-rectangular) arrays:
muon_pt = events['muon_pt'].array()
print(muon_pt)
[[53.4, 0.792], [30.1], [32.9, 0.769, 0.766], ... 40], [37.9], [35.2], [30.9, 3.59]]
We could get the number of muons in each collision with:
ak.num(muon_pt, axis=-1)
<Array [2, 1, 3, 1, 1, 1, ... 1, 1, 1, 1, 1, 2] type='15090 * int64'>
A quick note about axes in awkward: 0 is always the shallowest, while -1 is the deepest. In other words, axis=0 would tell us the number of subarrays (events), while axis=-1 would tell us the number of muons within each subarray. This array is only of dimension 2, so axis=1 or axis=-1 are the same. This usage is the same as for standard numpy arrays.
The traditional way of analyzing data in HEP involves the event loop. In this paradigm, we would write an explicit loop to go through every event (and through every field of an event that we wish to make a cut on). This method of analysis is rather bulky in comparison to the columnar approach, which (ideally) has no explicit loops at all! Instead, the fields of our data are treated as arrays and analysis is done by way of numpy-like array operations.
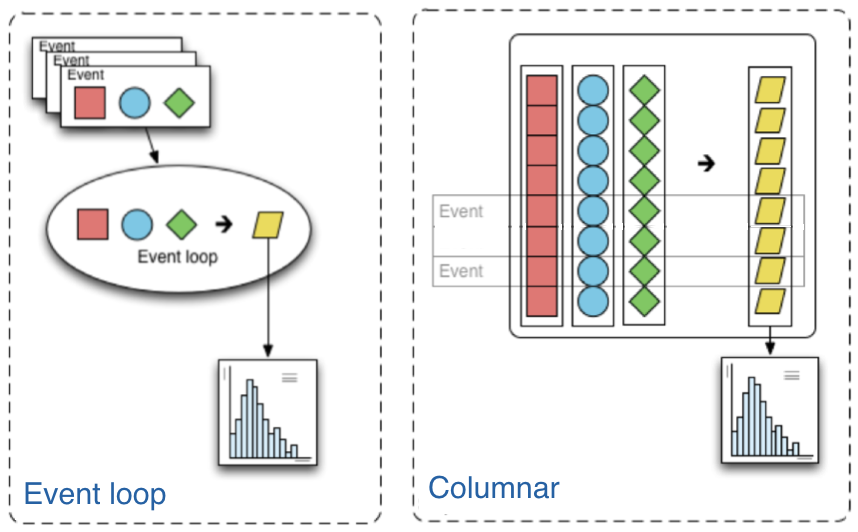
Most simple cuts can be handled by masking. A mask is a Boolean array which is generated by applying a condition to a data array. For example, if we want only muons with pT > 10, our mask would be:
print(muon_pt > 10)
[[True, False], [True], [True, False, False], ... [True], [True], [True, False]]
Then, we can apply the mask to our data. The syntax follows other standard array selection operations: data[mask]. This will pick out only the elements of our data which correspond to a True.
Our mask in this case must have the same shape as our muons branch, and this is guaranteed to be the case since it is generated from the data in that branch. When we apply this mask, the output should have the same amount of events, but it should down-select muons - muons which correspond to False should be dropped. Let’s compare to check:
print('Input:', muon_pt)
print('Output:', muon_pt[muon_pt > 10])
Input: [[53.4, 0.792], [30.1], [32.9, 0.769, 0.766], ... 40], [37.9], [35.2], [30.9, 3.59]]
Output: [[53.4], [30.1], [32.9], [28.3], [41.7], ... [42.6], [40], [37.9], [35.2], [30.9]]
We can also confirm we have fewer muons now, but the same amount of events:
print('Input Counts:', ak.sum(ak.num(muon_pt, axis=1)))
print('Output Counts:', ak.sum(ak.num(muon_pt[muon_pt > 10], axis=1)))
print('Input Size:', ak.num(muon_pt, axis=0))
print('Output Size:', ak.num(muon_pt[muon_pt > 10], axis=0))
Input Counts: 26690
Output Counts: 17274
Input Size: 15090
Output Size: 15090
Coffea
Awkward arrays let us access data in a columnar fashion, but that’s just the first part of doing an analysis. Coffea builds upon this foundation with a variety of features that better enable us to do our analyses. These features include:
-
Hists give us ROOT-like histograms. Actually, this is now a standalone package, but it has been heavily influenced by the (old) coffea hist subpackage, and it’s a core component of the coffea ecosystem.
-
NanoEvents and Schemas allows us to apply a schema to our awkward array. This schema imposes behavior that we would not have in a simple awkward array, but which makes our (HEP) lives much easier. On one hand, it can serve to better organize our data by providing a structure for naming, nesting, and cross-referencing fields; it also allows us to add physics object methods (e.g., for LorentzVectors).
-
Processors are coffea’s way of encapsulating an analysis in a way that is deployment-neutral. Once you have a Coffea analysis, you can throw it into a processor and use any of a variety of executors (e.g. Dask, Parsl, Spark) to chunk it up and run it across distributed workers. This makes scale-out simple and dynamic for users.
-
Lookup tools are available in Coffea for any corrections that need to be made to physics data. These tools read a variety of correction file formats and turn them into lookup tables.
In summary, coffea’s features enter the analysis pipeline at every step. They improve the usability of our input (NanoEvents), enable us to map it to a histogram output (Hists), and allow us tools for scaling and deployment (Processors).
Coffea NanoEvents and Schemas: Making Data Physics-Friendly
Before we can dive into our example analysis, we need to spruce up our data a bit.
Let’s turn our attention to NanoEvents and schemas. Schemas let us better organize our file and impose physics methods onto our data. There exist schemas for some standard file formats, most prominently NanoAOD (which will be, in the future, the main format in which CMS data will be made open), and there is a BaseSchema which operates much like uproot. The coffea development team welcomes community development of other schemas.
For the purposes of this tutorial, we already have a schema. Again, this was prepared already by Mat Adamec for the IRIS-HEP AGC Workshop 2022. Here, however, we will try to go into the details.
Before we start, don’t forget to include the libraries we need, including now the coffea ones:
import uproot
import awkward as ak
import hist
from hist import Hist
from coffea.nanoevents import NanoEventsFactory, BaseSchema
Remember the output we had above. After loading the file, we saw a lot of branches. Let’s zoom in on the muon-related ones here:
'numbermuon', 'nmuon_e', 'muon_e', 'nmuon_pt', 'muon_pt', 'nmuon_px', 'muon_px', 'nmuon_py', 'muon_py', 'nmuon_pz', 'muon_pz', 'nmuon_eta', 'muon_eta', 'nmuon_phi', 'muon_phi', 'nmuon_ch', 'muon_ch', 'nmuon_isLoose', 'muon_isLoose', 'nmuon_isMedium', 'muon_isMedium', 'nmuon_isTight', 'muon_isTight', 'nmuon_isSoft', 'muon_isSoft', 'nmuon_isHighPt', 'muon_isHighPt', 'nmuon_dxy', 'muon_dxy', 'nmuon_dz', 'muon_dz', 'nmuon_dxyError', 'muon_dxyError', 'nmuon_dzError', 'muon_dzError', 'nmuon_pfreliso03all', 'muon_pfreliso03all', 'nmuon_pfreliso04all', 'muon_pfreliso04all', 'nmuon_pfreliso04DBCorr', 'muon_pfreliso04DBCorr', 'nmuon_TkIso03', 'muon_TkIso03', 'nmuon_jetidx', 'muon_jetidx', 'nmuon_genpartidx', 'muon_genpartidx', 'nmuon_ip3d', 'muon_ip3d', 'nmuon_sip3d', 'muon_sip3d'
By default, uproot (and BaseSchema) treats all of the muon branches as distinct branches with distinct data. This is not ideal, as some of our data is redundant, e.g., all of the nmuon_* branches better have the same counts. Further, we’d expect all the muon_* branches to have the same shape, as each muon should have an entry in each branch.
The first benefit of instating a schema, then, is a standardization of our fields. It would be more succinct to create a general muon collection under which all of these branches (in NanoEvents, fields) with identical size can be housed, and to scrap the redundant ones. We can use numbermuon to figure out how many muons should be in each subarray (the counts, or offsets), and then fill the contents with each muon_* field. We can repeat this for the other branches.
We will, however, use a custom schema called AGCSchema, whose implementation resides in the agc_schema.py file you just downloaded.
Let’s open our example file again, but now, instead of directly using uproot, we use the AGCSchema class.
from agc_schema import AGCSchema
agc_events = NanoEventsFactory.from_root('root://eospublic.cern.ch//eos/opendata/cms/upload/od-workshop/ws2021/myoutput_odws2022-ttbaljets-prodv2.0_merged.root', schemaclass=AGCSchema, treepath='events').events()
For NanoEvents, there is a slightly different syntax to access our data. Instead of querying keys() to find our fields, we query fields. We can still access specific fields as we would navigate a dictionary (collection[field]) or we can navigate them in a new way: collection.field.
Let’s take a look at our fields now:
agc_events.fields
['muon', 'fatjet', 'jet', 'photon', 'electron', 'tau', 'met', 'trig', 'btag', 'PV']
We can confirm that no information has been lost by querying the fields of our event fields:
agc_events.muon.fields
['pt', 'px', 'py', 'pz', 'eta', 'phi', 'ch', 'isLoose', 'isMedium', 'isTight', 'isSoft', 'isHighPt', 'dxy', 'dz', 'dxyError', 'dzError', 'pfreliso03all', 'pfreliso04all', 'pfreliso04DBCorr', 'TkIso03', 'jetidx', 'genpartidx', 'ip3d', 'sip3d', 'energy']
So, aesthetically, everything is much nicer. If we had a messier dataset, the schema can also standardize our names to get rid of any quirks. For example, every physics object property in our tree has an n* variable which, if you were to check their values, you would realize that they repeat. They give just the number of objects in the field. We need only one variable to check that, and for the muons would be numbermuon. This sort of features are irrelevant after the application of the schema, so we don’t have to worry about it.
There are also other benefits to this structure: as we now have a collection object (agc_events.muon), there is a natural place to impose physics methods. By default, this collection object does nothing - it’s just a category. But we’re physicists, and we often want to deal with Lorentz vectors. Why not treat these objects as such?
This behavior can be built fairly simply into a schema by specifying that it is a PtEtaPhiELorentzVector and having the appropriate fields present in each collection (in this case, pt, eta, phi and e). This makes mathematical operations on our muons well-defined:
agc_events.muon[0, 0] + agc_events.muon[0, 1]
<LorentzVectorRecord ... y: -17.7, z: -11.9, t: 58.2} type='LorentzVector["x": f...'>
And it gives us access to all of the standard LorentzVector methods, like \(\Delta R\):
agc_events.muon[0, 0].delta_r(agc_events.muon[0, 1])
2.512794926098977
We can also access other LorentzVector formulations, if we want, as the conversions are built-in:
agc_events.muon.x, agc_events.muon.y, agc_events.muon.z, agc_events.muon.mass
/usr/local/venv/lib/python3.10/site-packages/awkward/_connect/_numpy.py:195: RuntimeWarning: invalid value encountered in sqrt
result = getattr(ufunc, method)(
(<Array [[50.7, 0.0423], ... [21.1, -1.38]] type='15090 * var * float32'>, <Array [[-16.9, -0.791], ... [-22.6, 3.31]] type='15090 * var * float32'>, <Array [[-7.77, -4.14], ... [-11, -6.83]] type='15090 * var * float32'>, <Array [[0.103, 0.106], ... [0.105, 0.106]] type='15090 * var * float32'>)
NanoEvents can also impose other features, such as cross-references in our data; for example, linking the muon jetidx to the jet collection. This is not implemented in our present schema.
Let’s take a look at the agc_schema.py file
Anyone, in principle, can write a schema that suits particular needs and that could be plugged into the coffea insfrastructure. Here we present a challenge to give you a felling of the kind of arrangements schemas can take care of.
Challenge: Adding the corrected jet energy to the LorentzVector
If you check the variables above, you will notice that the
jetobject has an energyerecorded but also, as you learn from the physics objects lesson,corre, which is the corrected energy. You can also realize about this if you dump the fields for the jet:agc_events.jet.fieldsYou should find that you can see the
correvariable, but this should not happen because it should have been recorded asenergyfor the LorentzVector funcionality.Inspect and study the file
agc_schema.pyto fix this problem and pass thiscorreenergy as the energy to the LorentzVector and not the uncorrectedeenergy. The changes for_eshould remain valid for the rest of the objects though. Note that you could correct for thefatjetalso in the same line of action.In order to see the difference you need to reload the schema. It may be necessary to rm the
__pycache__directory in your area altogether.Solution
You can download the solution from here
Key Points
We will be perfoming a real but simplified HEP analysis using CMS Run2 open data using columnar analysis.
Coffea is a framework which builds upons several tools to make columnar analysis more efficient in HEP.
Schemas are a simple way of rearranging our data content so it is easier to manipulate